COMPUTER AIDED ARCHITECTURAL DESIGN
 Workshop 19 Notes, Week of November 16, 2020

GEODESIC OCTAHEDRON AND ICOSAHEDRON POLYGON SURFACES THROUGH SPHERICAL PROJECTION

The geodesic geometry illustrated here is based on the two cases of the Octahedron and of the Icosahedron in parts 2 and 3 below. These workshop notes are intended to supplement the introduction to this geodesic geometry in the workhops directly, and do not replace the workshops completely.

These workshop notes also continue with polygon surfaces based upon points, and point indexes described below, They introduce methods of spherical projection to produce the geodesic Octahedron and a geodesic Icosahedron. The means of projection spherically take into account a different approach than the vertical projection which was developed previously for the polygon surfaces for the polynomial expressions.

In the examples below, polygons are again described with reference to the World Coordinate System. The example grasshopper scripts are posted to the CLASSES/EXAMPLES folder for ARCH 2710 under the sub-folder named "geodesic" and in the Collab site resources folder. You can simply run the Python components as provided or follow the details more closely below. To activate any of the components right-mouse-button click on it and turn the Preview option. The code uses recursive programming. The method of accounting for the geometry of mesh surfaces in this example is lower level and more complex than other examples. It is extracurricular in terms of the details, but the Python components as posted may still be relelatively easy to use otherwise.

PART 1. Polygon Surfaces Based Upon Vertices, Faces and Surface Normals.

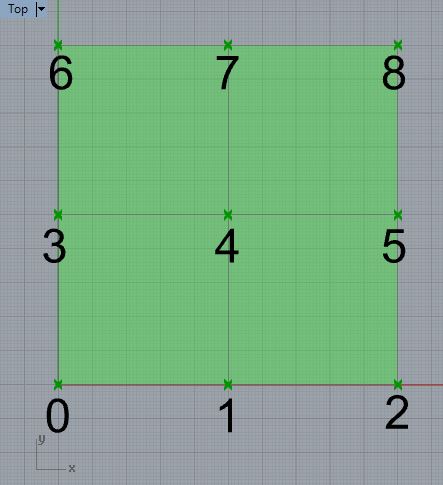
In the following figure, there are nine vertices, labelled 0 through 8,  and four associated faces determined by indexes to the vertices (0, 1, 4, 3), (1, 2, 5, 4), (3, 4, 7, 6) and (4, 5, 8, 7). To generate the surface, we need a way to organize every four adjacent vertices such that they form the individual grid faces that constitute the overall surface. Thus a list of all the vertices and separate list consisting of an indexing system that determines all the subgroups of 4 vertices forming each face are both needed. (This example is modified after a rhinoscriptsyntax help example provided by McNeel Inc.). In addition, the indexes to the vertices are listed in counter clock-wise order such as in the case of vertices 0, 1, 4, 3 beginning with the lower left-hand vertice 0.

four faces

A Python script to generate the polygon mesh surface and index into the vertices would be as follows.  Note that the "faceVertices" array contains a list of  index locations in the "vertices" array for each face of the polygon mesh. 

import rhinoscriptsyntax as rs
import Rhino as rh

#vertices of polygon mesh
pt0 = rh.Geometry.Point3d(0, 0, 0)
pt1 = rh.Geometry.Point3d(5, 0, 0)
pt2 = rh.Geometry.Point3d(10, 0, 0)
pt3 = rh.Geometry.Point3d(0, 5, 0)
pt4 = rh.Geometry.Point3d(5, 5, 0)
pt5 = rh.Geometry.Point3d(10, 5, 0)
pt6 = rh.Geometry.Point3d(0, 10, 0)
pt7 = rh.Geometry.Point3d(5, 10, 0)
pt8 = rh.Geometry.Point3d(10, 10, 0)
#create array of vertices
vertices = [pt0, pt1, pt2, pt3, pt4, pt5, pt6, pt7, pt8]

#create index into vertices array to determine faces
faceVertices = []
faceVertices.append((0,1,4,3))
faceVertices.append((1,2,5,4))
faceVertices.append((3,4,7,6))
faceVertices.append((4,5,8,7))

a = rs.AddMesh( vertices, faceVertices ) #output variable a
b = vertices #output variable b

However, in order to control the visibility of polygon surface sphere, the script also adds a vector direction property for each of its vertex points. That is, a positive vector pointing perpendicularly outward from the vertex points on the surface makes the sphere visible when viewed from the outside. This vector pointing perpendicularly outward from the surface is typically referred to as the "surface normal". Thus, in the trivial case of the four faces in the example above, for each vertex we create a positive set of positive vectors "vN" all exactly the same and facing upward in the direction (0, 0, 1) as indicated in the grey text box below.  

The vectors are placed in a list named "normals" within the script as follows:

#create array of surface Normals
vN = rh.Geometry.Vector3d(0,0,1)
normals = [vN, vN, vN, vN, vN, vN, vN, vN, vN]

In turn, the "normals" are incorporated incorporated into the polygon surface with the call to the AddMesh function:

a = rs.AddMesh( vertices, faceVertices, normals ) #output variable a with "normals" added to the AddMesh function


import rhinoscriptsyntax as rs
import Rhino as rh

#vertices of polygon mesh
pt0 = rh.Geometry.Point3d(0, 0, 0)
pt1 = rh.Geometry.Point3d(5, 0, 0)
pt2 = rh.Geometry.Point3d(10, 0, 0)
pt3 = rh.Geometry.Point3d(0, 5, 0)
pt4 = rh.Geometry.Point3d(5, 5, 0)
pt5 = rh.Geometry.Point3d(10, 5, 0)
pt6 = rh.Geometry.Point3d(0, 10, 0)
pt7 = rh.Geometry.Point3d(5, 10, 0)
pt8 = rh.Geometry.Point3d(10, 10, 0)
#create array of vertices
vertices = [pt0, pt1, pt2, pt3, pt4, pt5, pt6, pt7, pt8]

#create array of surface Normals
vN = rh.Geometry.Vector3d(0,0,1)
normals = [vN, vN, vN, vN, vN, vN, vN, vN, vN]

#create index into vertices array to determine faces
faceVertices = []
faceVertices.append((0,1,4,3))
faceVertices.append((1,2,5,4))
faceVertices.append((3,4,7,6))
faceVertices.append((4,5,8,7))

a = rs.AddMesh( vertices, faceVertices, normals ) #output variable a with "normals" added to AddMesh function
b = vertices #output variable b


Similarly, in the examples developed for this tutorial, the surface normals are added to the rhinoscriptsyntax function which generates the polygonal surface for the geodesic forms.

 PART 2. Geodesic Octahedron Polygon Surfaces Based Upon Vertices, Faces and Surface Normals.

We can initiate an Octahedron as a visaul sequence with three lines relative to the origin with radius of 1.0 along the X, Y, and Z axis as in the figure below.

three axial lines


Connecting the end points of horizontal linesin the X-Y plane with the vertical line on the Z-axis creates one pyramid sitting on top of its mirror, or the base shape of an Octahedron.

octahedron

 Note that the three corner points of each face need to be assembled in counter-clockwise order when viewed from the outside to the inside of the Octahedron looking towards its interior centerpoint. By convention this means that the face is viewed as a surface rather than as a hole. Thus, for the outer triangulated surface directly oriented to the screen in the perspective window in the image above, where the red line represents the positive x-axis and thee green line represents the positive y-axis,  the 3 points would be in the (x, y, z) order of    (-1, 0, 0) ,  (0, -1, 0), and  (0, 0, 1). This order in turn would also be true of any surfaces to be formed by  subdivided triangles of the same face.


Using a recursive method, subdividing each triangular face into four trianges at a rcursive level 2 of the Octahedron establishes a triangle grid as indicated in the following ima

subdivided face recursion 2


At recursive levels of 3, 4, and 5, the following results are obtained. We move from having just 8 triangles overall at  level of recursion 1 to 2048 at level of recursion 8.

recursive level 3 recursive level 4 recursive level 5
recursive level 3 recursive level 4 recursive level 5



However, stepping back to recursive level 2,  now create a vector going from the center (e.g, the point 0,0,0)  of the Octahedron to each corner point on each triangle on each face of the Octahedron. In the following example we create a vector from the origin to just one of the triangle corner point vertices.

vector to vertice


Next, assume that each such vector is resized to a vector of length 1 as in the next illustration.

change to unit vector

To arrive at a spherical projection,  for each such unit vector for every corner vertice on each triangle, multiply the unit vector  by whatever size radius is desired. Project the vertices at the  radius distance of 1, and you get the projection indicated in the following figure.

radius 1 projection

At radius 2, the projection would appear as follows.

projection at radius 2

If each triangle's corner points generates a surface facet  then from the last projection at radius 2 we would get the following result.
radius 2 surf recursive level 3 radius 2 shaded
recursive level 3 radius 2 transparent shadeding recursive level 3 radius 2 opaque shading


At recursive levels 4 and 5 we get the following surface geometry.
radius 2 surf radius 2 surf
recursive level 4 radius 2 recursive level 5 radius 2

The Grasshopper Python Script Used to Generate thissequence begins with a point at the origin of the Cartesian Coordinate Space in Rhino.

center pt

The Python script itself has input parameters for:

centerPt - the point at the origin above
radius - the floating point (i.e., decimal point) radius of the geodesic Octahedron
recur - the integer (i.e., whoe number) level of recursion of the projected triangulated surface of the geodesic Octahedron.

The output parameters are:

a = polygon mesh surface
c = centroid of each trianglar facet in the surface
n = surface normal at each centroid

octahedron canvas window

The Grasshopper file can be downloaded from the link geodesicOctahedronSurfCN.gh. The details are too extensive to described in these notes, but will be summarized at greater depth within the workshop itself. The Python script is itself is reproduced below; however, the main objective here is to understand the projective illustrations above and not necessarily to be able to independently reproduce the Python script as documented below.  Note that one of the functions " def buildPolysurf(projTPts, centerPt)" includes some code to add outwardly projected surface normals to the mesh similar to the simpler case descibed above in part 1.
#create geodesic octahedron by radial projection based upon recursive triangles
#Earl Mark 11.25.17
import rhinoscriptsyntax as rs
import Rhino as rh

def paramPt(ptA, ptB, param):
    #get parametric point from ptA to ptB
    x = ptA.X + (ptB.X - ptA.X) * param
    y = ptA.Y + (ptB.Y - ptA.Y) * param
    z = ptA.Z + (ptB.Z - ptA.Z) * param
    pt = rh.Geometry.Point3d(x, y, z)
    return pt

def getCentroid(ptList):
    #get centroid of a point list
    x = 0
    y = 0
    z = 0
    for pt in ptList:
        x += pt.X
        y += pt.Y
        z += pt.Z
    cPt = rh.Geometry.Point3d(x/len(ptList), y/len(ptList) , z/len(ptList))
    return cPt

def getAxisPts(centerPt):
    #gets axis pts at 1 unit radial dimensions in X, Y and Z
    xAPt1 = rh.Geometry.Point3d(centerPt.X - 1, centerPt.Y, centerPt.Z)
    xAPt2 = rh.Geometry.Point3d(centerPt.X + 1, centerPt.Y, centerPt.Z)
    yAPt1 = rh.Geometry.Point3d(centerPt.X, centerPt.Y - 1, centerPt.Z)
    yAPt2 = rh.Geometry.Point3d(centerPt.X, centerPt.Y + 1, centerPt.Z)
    zAPt1 = rh.Geometry.Point3d(centerPt.X, centerPt.Y, centerPt.Z - 1)
    zAPt2 = rh.Geometry.Point3d(centerPt.X, centerPt.Y, centerPt.Z + 1)
    return [xAPt1, xAPt2, yAPt1, yAPt2, zAPt1, zAPt2]

def formOctantTriangles(axisPts):
    #determine three corner points for each triangle in each octant of the octahedron
    #start in -z area and counter clockwise at lower left in plan
    #and then similarly +z area counter clockwise at lower left in plan
    #in addition, each set of three triangular points must be assembled in counter-clockwise order
    #when view from outside the Octrahedron towards the interior center
    #negative z triangles
    lLeftNz = [axisPts[4],axisPts[2],axisPts[0]]
    lRightNz = [axisPts[4],axisPts[1], axisPts[2]]
    uRightNz = [axisPts[4],axisPts[3], axisPts[1]]
    uLeftNz = [axisPts[4],axisPts[0], axisPts[3]]
    #positive z triangles
    lLeftPz = [axisPts[0],axisPts[2],axisPts[5]]
    lRightPz = [axisPts[2],axisPts[1], axisPts[5]]
    uRightPz = [axisPts[1],axisPts[3], axisPts[5]]
    uLeftPz = [axisPts[3],axisPts[0], axisPts[5]]
    return [lLeftNz, lRightNz, uRightNz, uLeftNz, lLeftPz, lRightPz, uRightPz, uLeftPz]

def subdivideTrianglePts(trianglePts):
    #divide one triangle's pts into 4 sets of
    #triangle pts including center triangle
    pt1 = trianglePts[0]
    pt2 = trianglePts[1]
    pt3 = trianglePts[2]
    #determine the midpoints of the three initial corner points
    pt1m = paramPt(pt1, pt2, 0.5)
    pt2m = paramPt(pt2, pt3, 0.5)
    pt3m = paramPt(pt3, pt1, 0.5)
    #determine the four triangles obtained by subdividing the original triangle
    lleftT = [pt1, pt1m, pt3m]
    lrightT = [pt1m, pt2, pt2m]
    apexT = [pt3m, pt2m, pt3]
    cenT = [pt3m, pt1m, pt2m]
    return [lleftT, lrightT, apexT, cenT]

def subTriPtRecursive(trianglePts, recur, triangleList):
    #divides triangles on geodesic surface recursively
    if (recur == 1):
        #if recursion is complete then return the triangle points
        triangleList.append(trianglePts)
    else:
        #if more recursion to do, then continue to subdivide each triangle
        newTriangles = subdivideTrianglePts(trianglePts)
        triangleList = subTriPtRecursive(newTriangles[0], recur - 1, triangleList) #lower left triangle
        triangleList = subTriPtRecursive(newTriangles[1], recur - 1, triangleList) #lower right triangle
        triangleList = subTriPtRecursive(newTriangles[2], recur - 1, triangleList) #apex triangle
        triangleList = subTriPtRecursive(newTriangles[3], recur - 1, triangleList) #center triangle
    return triangleList

def subTriPtRecurOctants(octantsTriPts, recur, triangleList):
    #initiate recursive subdivide for each octants original triangle of pts
    for octT in octantsTriPts:
        triangleList = subTriPtRecursive(octT, recur, triangleList)
    return triangleList

def projectPts(allTrianglePts, centerPt, r):
    #project all triangular faces to a spherical coordinate based upon the radius r
    projTPts = []
    cX = centerPt.X
    cY = centerPt.Y
    cZ = centerPt.Z
    for t in allTrianglePts:
        pt1 = t[0]
        pt2 = t[1]
        pt3 = t[2]
        v1 = rh.Geometry.Vector3d(pt1.X - cX, pt1.Y - cY, pt1.Z - cZ)
        v2 = rh.Geometry.Vector3d(pt2.X - cX, pt2.Y - cY, pt2.Z - cZ)
        v3 = rh.Geometry.Vector3d(pt3.X - cX, pt3.Y - cY, pt3.Z - cZ)
        v1.Unitize()
        v2.Unitize()
        v3.Unitize()
        tP1 = rh.Geometry.Point3d(v1.X * r + cX,v1.Y * r + cY, v1.Z * r + cZ)
        tP2 = rh.Geometry.Point3d(v2.X * r + cX,v2.Y * r + cY, v2.Z * r + cZ)
        tP3 = rh.Geometry.Point3d(v3.X * r + cX,v3.Y * r + cY, v3.Z * r + cZ)
        projTPts.append([tP1, tP2, tP3])
    return projTPts

def buildPolysurf(projTPts, centerPt):
    #build faces, center points and center point surface normals
    i = 0 #initiate index counter for each corner vertex for triangle
    indexList = []
    ptList = []
    vertexNormals = [] #to store normal vectors to each point for each face
    vecNCs = [] #to store normal vectors for each centroid of each face
    cPts = [] #to store center point of each face
    for t in projTPts:
        curSurfIndex = [i, i + 1, i + 2]
        indexList.append(curSurfIndex)
        ptList.append(t[0])
        ptList.append(t[1])
        ptList.append(t[2])
        cPt = getCentroid([t[0],t[1],t[2]])
        cPts.append(cPt)
        #get vector from center point of octahedron to center point of unprojected face
        vecN = rh.Geometry.Vector3d(cPt.X - centerPt.X,cPt.Y - centerPt.Y,cPt.Z - centerPt.Z)
        #change length of vector to 1 unit
        vecN.Unitize()
        #round out vector components to two signicant digits (e.g, 1.23)
        vecN = rh.Geometry.Vector3d(round(vecN.X, 2), round(vecN.Y, 2), round(vecN.Z, 2))
        #store centerpoint of each face
        cPts.append(cPt)
        #store vector normal for each vertex of each face
        vertexNormals.append(vecN)
        vertexNormals.append(vecN)
        vertexNormals.append(vecN)
        #store vector normal for centroid of each face
        vecNCs.append(vecN)
        i += 3
    #create the surface
    surf1 = rs.AddMesh(ptList,indexList,vertexNormals)
    return [surf1, cPts, vecNCs]

#main
#get the axis points determining initial octahedron
axisPts = getAxisPts(centerPt)
#determine cornerpoints of each facet of initial octahedron (number of facets is 8)
trianglePts = formOctantTriangles(axisPts)
octantsTriPts = trianglePts
#store all the triangle points for subdivided faces of initial octahedron
allTrianglePts = []
#recursively subdivide primary points of faces of initial octahedron
allTrianglePts = subTriPtRecurOctants(octantsTriPts, recur, allTrianglePts)
#project all the points of the octahedron spherically
projAllTPoints = projectPts(allTrianglePts, centerPt, radius)
#build the polygon surface mesh for the geodesic octahedron
surfData = buildPolysurf(projAllTPoints, centerPt)

a = surfData[0] #mesh surface
c = surfData[1] #mesh face centerPts
n = surfData[2] #mesh face normals

print("Number faces " + str(len(n)))

 PART 3. Geodesic Icosahedron Polygon Surfaces Based Upon Vertices, Faces and Surface Normals.

The projective techniques used to build a Geodesic Icosahedron here are similar to the sequence used  to buid the Geodesic Ocrtahedron above. We begin with three golden rectangles at right angles to each other and centered on the origin (x = 0, y = 0, z = 0) of the Cartesian coordinate system in Rhino..

3 golden rectangles

Note that the diagonal radius from the center of each golden rectangle to any of its corner depicted in orange below is set to the unit size of 1.

golden rectangle radius


Connecting adjacent vertices of three goldern golden rectangles in the triangular manner illustrated in the next figure we get 20 tringulated faces.  Note that the radius of each corner vertice of the triangle is the same as the diagonal radius of the golden rectangles.  That is, using the previous golden rectangles, the radius of each of the corner vertices from the origin of the Cartesian coordinate system is 1.

triangulated corners

Similar to the Octahedron we can recursively subdivide each triangle as in the following two cases for recursion = 3, 4, and 5. In the case of going from recursion level 1 to  recursion level 5 we go from 20 total triangles to 5120 triangles. 

recursive level 3 recursive level 4 recursive level 5
recursive level 3 recursive level 4 recursive level 5

Using the same method of projection developed for the Octahedron, we can spherically project each of the trianglular vertices at a radial values. Project the vertices at the  radius distance of 1, and you get the projection indicated in the following figure.

radius 1 projection


At radius 2, the projection would appear as follows.

projection at radius 2

 If each triangle's corner points generates a surface facet  then from the last projection at radius 2 we would get the following result.
radius 2 surf recursive level 3 radius 2 shaded
recursive level 3 radius 2 recursive level 3 radius 2


At recursive levels 4 and 5 we get the following surface geometry.
radius 2 surf radius 2 surf
recursive level 4 radius 2 recursive level 5 radius 2

The Grasshopper Python Script Used to generate this sequence begins with a point at the origin of the Cartesian Coordinate Space in Rhino.

center pt

The Python script itself has input parameters for:

centerPt - the point at the origin above
radius - the floating point (i.e., decimal point) radius of the geodesic Icosahedron
recur - the integer level of recursion of the projected triangulated surface  of the geodesic Icosahedron.
displayGeodesic - boolean value to display the primary geometry of the mesh surface, centroids of each triangle and surface normals for each surfrace normal
displayCE -  boolean value to display the  interim constructive geometry including the the intial base Icoashedron, the non-projected triangles, and the sperically projected triangles.

The output parameters are divided into two parts:

1. Primary Elements:
m = polygon mesh surface
c = centroid of each trianglar facet in the surface
n = surface normal at each centroid

2. Interim Construction Elements
i = base Icosahedron unprojected at radius 1
g = goldern rectangles
t = triangles


icosahedron canvas window

The Grasshopper file can be downloaded from the link for the geodesicIcosahedronRecursiveProjCN.gh. The details are too numerous to described in these notes, but will be summarized at greater depth within the workshop itself. The Python script is itself is reproduced below; however, the main objective here is to understand the projective illustrations above and not necessarily to be able to indentently reproduce the Python script as documented below.   Note that one of the functions " def buildPolysurf(projTPts, centerPt)" includes some code to add outwardly projected surface normals to the mesh similar to the simpler case descibed above in part 1. Moreover, most of the functions used in the case of the Octahedron are also used here.
#Geodesic Icosahedron By Projection From Golden Rectangles
#Earl Mark 11.25.17
import Rhino as rh
import rhinoscriptsyntax as rs
import math

def paramPt(ptA, ptB, param):
    #get parametric point from ptA to ptB
    x = ptA.X + (ptB.X - ptA.X) * param
    y = ptA.Y + (ptB.Y - ptA.Y) * param
    z = ptA.Z + (ptB.Z - ptA.Z) * param
    pt = rh.Geometry.Point3d(x, y, z)
    return pt

def getCentroid(ptList):
    #get centroid of a point list
    x = 0
    y = 0
    z = 0
    for pt in ptList:
        x += pt.X
        y += pt.Y
        z += pt.Z
    cPt = rh.Geometry.Point3d(x/len(ptList), y/len(ptList) , z/len(ptList))
    return cPt

def subdivideTrianglePts(trianglePts):
    #divide one triangle's pts into 4 sets of
    #triangle pts including center triangle
    pt1 = trianglePts[0]
    pt2 = trianglePts[1]
    pt3 = trianglePts[2]
    #get mid points of each side
    pt1m = paramPt(pt1, pt2, 0.5)
    pt2m = paramPt(pt2, pt3, 0.5)
    pt3m = paramPt(pt3, pt1, 0.5)
    #determine four triangles
    lleftT = [pt1, pt1m, pt3m]
    lrightT = [pt1m, pt2, pt2m]
    apexT = [pt3m, pt2m, pt3]
    cenT = [pt3m, pt1m, pt2m]
    return [lleftT, lrightT, apexT, cenT]

def subTriPtRecursive(trianglePts, recur, triangleList):
    #divides triangles on geodesic surface recursively
    if (recur == 1):
    #if finished with recursion (recur == 1) return final set of points
        triangleList.append(trianglePts)
    else:
    #if not finished with recursion (recur > 1) then continue to subivide
        newTriangles = subdivideTrianglePts(trianglePts)
        triangleList = subTriPtRecursive(newTriangles[0], recur - 1, triangleList) #lower left triangle
        triangleList = subTriPtRecursive(newTriangles[1], recur - 1, triangleList) #lower right triangle
        triangleList = subTriPtRecursive(newTriangles[2], recur - 1, triangleList) #apex triangle
        triangleList = subTriPtRecursive(newTriangles[3], recur - 1, triangleList) #center triangle
    return triangleList

def subTriPtRecurOnPrimary(octantsTriPts, recur, triangleList):
    #initiate recursive subdivide for each octants original triangle of pts
    for primaryT in octantsTriPts:
        triangleList = subTriPtRecursive(primaryT, recur, triangleList)
    return triangleList

def drawGRectPts(ctrPt):
    #draw a golden rectangle's points such that ctrPt to corner radius is 1
    #use ratios size rectangle
    distL1 = (1 + math.sqrt(5.0))/2.0 
    distR2 = 1 
    distD1 = 1
    distR1 = math.sqrt(pow(distL1, 2) + pow(distD1, 2))
    distL2 = distR2/distR1 * distL1
    distD2 = distR2/distR1 * distD1
    w = 2 * distL2
    d = 2 * distD2
    #establish corner points
    pt1 = rh.Geometry.Point3d(ctrPt.X - 0.5 * w, ctrPt.Y - 0.5 * d, ctrPt.Z)
    pt2 = rh.Geometry.Point3d(ctrPt.X + 0.5 * w, ctrPt.Y - 0.5 * d, ctrPt.Z)
    pt3 = rh.Geometry.Point3d(ctrPt.X + 0.5 * w, ctrPt.Y + 0.5 * d, ctrPt.Z)
    pt4 = rh.Geometry.Point3d(ctrPt.X - 0.5 * w, ctrPt.Y + 0.5 * d, ctrPt.Z)
    pts = [pt1, pt2, pt3, pt4]
    #For debugging, dislay golden rectangle's surface
    #faces = []
    #faces.append([0, 1, 2, 3])
    #gRec = rs.AddMesh(pts, faces)
    return pts

def rotatePts(ptList, ctrPt, axisVec, angle):
    #rotate corner pts of Golden Rectangle on x-y plane (used to determine other two golden rectangles)
    newPts = []
    for pt in ptList:
        ptNew = rs.AddPoint(pt.X, pt.Y, pt.Z)
        ptNew = rs.RotateObject(ptNew, ctrPt, angle ,axis = axisVec, copy = True)
        ptNew = rs.coerce3dpoint(ptNew) #return point as Rhino point (not Rhinoscriptsyntax point)
        newPts.append(ptNew)
    return newPts

def drawGoldenRects(ctrPt):
    #creates points and mesh surfaces of the three golden retangles
    #get the point of the golden rectangle in the x-y plane
    pts1 = drawGRectPts(ctrPt)
    #determine three axis of rotation used
    xVec = rh.Geometry.Vector3d(1, 0, 0)
    yVec = rh.Geometry.Vector3d(0, 1, 0)
    zVec = rh.Geometry.Vector3d(0, 0, 1)
    angle = 90
    ptsT = rotatePts(pts1,ctrPt, xVec, angle)
    #use rotation to get golden rectangle in y-z plane
    pts2 = rotatePts(ptsT,ctrPt,zVec, angle)
    #use rotation to get golden rectangle in x-z plane
    pts3 = rotatePts(ptsT,ctrPt,yVec, -angle)
    faces = []
    faces.append([0, 1, 2, 3])
    mesh1 = rs.AddMesh(pts1,faces)
    mesh2 = rs.AddMesh(pts2,faces)
    mesh3 = rs.AddMesh(pts3,faces)
   
    return pts1, pts2, pts3, mesh1, mesh2, mesh3

def drawPrimeIcosahedron(pts1, pts2, pts3):
    #draw bottom and mid level triangles counter clockwise from lower left
    #then draw upper level triangles in similar order
    #in addition, each set of three triangular points must be assembled in counter-clockwise order
    #when view from outside the Octrahedron towards the interior center
    #
     #lists of 20 sets of triangular pts flattened on primary icosahedron
    tList = []
    tList.append([pts3[3],pts2[0],pts1[0]])
    tList.append([pts2[0],pts2[3],pts1[0]])
    tList.append([pts3[3],pts3[0],pts2[0]])
    tList.append([pts2[0],pts1[1],pts2[3]])
    tList.append([pts3[0],pts1[1],pts2[0]])
    tList.append([pts3[0],pts1[2],pts1[1]])
    tList.append([pts3[0],pts2[1],pts1[2]]) # 8 5 2
    tList.append([pts2[1],pts2[2],pts1[2]])
    tList.append([pts3[0],pts3[3],pts2[1]])
    tList.append([pts2[1],pts1[3],pts2[2]])
    tList.append([pts3[3],pts1[3],pts2[1]])
    tList.append([pts1[3],pts1[0],pts3[2]])
    tList.append([pts1[0],pts2[3],pts3[2]])
    tList.append([pts2[3],pts3[1],pts3[2]])
    tList.append([pts1[1],pts1[2],pts3[1]])
    tList.append([pts1[2],pts2[2],pts3[1]])
    tList.append([pts2[2],pts3[2],pts3[1]])
    tList.append([pts1[3],pts3[2],pts2[2]])
    tList.append([pts1[1],pts3[1],pts2[3]])
    tList.append([pts3[3],pts1[0],pts1[3]])
   
    #faceList indices (indices of 20 triangular facets) on primary icosahedron
    faceList = []
    faceList.append([11,4,0]) 
    faceList.append([11, 0, 3])
    faceList.append([4, 7, 0])
    faceList.append([11, 8, 4])
    faceList.append([4, 1, 7])
    faceList.append([8, 1, 4])
    faceList.append([8, 2, 1])
    faceList.append([8, 5, 2])
    faceList.append([5, 6, 2])
    faceList.append([8, 11, 5])
    faceList.append([5, 3, 6])
    faceList.append([11, 3, 5])
    faceList.append([3, 0, 10])
    faceList.append([0, 7, 10])
    faceList.append([7, 9, 10])
    faceList.append([1, 9, 7]) 
    faceList.append([1, 2, 9])
    faceList.append([2, 6, 9])
    faceList.append([6, 10, 9])
    faceList.append([3, 10, 6])
   
   
    #point list forming base rectangles of icosahedron and index numerical order in comment lines above
    #index        0        1           2          3           4           5           6           7          8          9          10         11
    ptList = [pts1[0], pts1[1], pts1[2], pts1[3], pts2[0], pts2[1], pts2[2], pts2[3], pts3[0], pts3[1], pts3[2], pts3[3]]
    #create icosahedron poly mesh
    mesh1 = rs.AddMesh(ptList, faceList)
    return tList, mesh1 #return initial triangle point list, initial mesh.

def projectPts(allTrianglePts, centerPt, r):
    #project all triangular faces to a spherical vertices based upon the radius r
    projTPts = []
    cX = centerPt.X
    cY = centerPt.Y
    cZ = centerPt.Z
    #for each corner pt of each triangle
    for t in allTrianglePts:
        pt1 = t[0]
        pt2 = t[1]
        pt3 = t[2]
        #determine a vector from the centerPt to each point
        v1 = rh.Geometry.Vector3d(pt1.X - cX, pt1.Y - cY, pt1.Z - cZ)
        v2 = rh.Geometry.Vector3d(pt2.X - cX, pt2.Y - cY, pt2.Z - cZ)
        v3 = rh.Geometry.Vector3d(pt3.X - cX, pt3.Y - cY, pt3.Z - cZ)
        #unitize each vector (so that it has length 1)
        v1.Unitize()
        v2.Unitize()
        v3.Unitize()
        #multiple vector x, y, z component by the radius and add to the centerPt
        tP1 = rh.Geometry.Point3d(v1.X * r + cX,v1.Y * r + cY, v1.Z * r + cZ)
        tP2 = rh.Geometry.Point3d(v2.X * r + cX,v2.Y * r + cY, v2.Z * r + cZ)
        tP3 = rh.Geometry.Point3d(v3.X * r + cX,v3.Y * r + cY, v3.Z * r + cZ)
        projTPts.append([tP1, tP2, tP3])
    return projTPts

def buildPolysurf(projTPts, centerPt):
    #build faces, center points and center point surface normals
    i = 0
    s = 0
    indexList = []
    ptList = []
    vertexNormals = []
    vecNCs = []
    cPts = []
    surfs = []
    for t in projTPts:
        curSurfIndex = [i, i + 1, i + 2]
        indexList.append(curSurfIndex)
        ptList.append(t[0])
        ptList.append(t[1])
        ptList.append(t[2])
        cPt = getCentroid([t[0],t[1],t[2]])
        cPts.append(cPt)
        vecN = rh.Geometry.Vector3d(cPt.X - centerPt.X,cPt.Y - centerPt.Y,cPt.Z - centerPt.Z)
        vecN.Unitize()
        vecN = rh.Geometry.Vector3d(round(vecN.X, 2), round(vecN.Y, 2), round(vecN.Z, 2))
        cPts.append(cPt)
        #Duplicate surface normal for each tiangle vertex of a given face
        vertexNormals.append(vecN)
        vertexNormals.append(vecN)
        vertexNormals.append(vecN)
        #Save surface normal for each centroid of a given face
        vecNCs.append(vecN)
        i += 3
    #build the polygon mesh surface with surface normals pointing out and away from centerPt
    #surface normals by convention determine positive and visible side of surface
    surf1 = rs.AddMesh(ptList,indexList,vertexNormals)
    return [surf1, cPts, vecNCs]

def displayPrimaryTrianglePts(allTrianglePts):
    flatPolyLineList = []
    for tri in allTrianglePts:
        pline = rs.AddPolyline([tri[0], tri[1], tri[2], tri[0]])
        flatPolyLineList.append(pline)
    return flatPolyLineList


#main
#create Golden Retangles
grLists = drawGoldenRects(ctrPt)
pts1 = grLists[0]
pts2 = grLists[1]
pts3 = grLists[2]
mesh1 = grLists[3]
mesh2 = grLists[4]
mesh3 = grLists[5]


#draw primary icosahedron at radius 1
iCos = drawPrimeIcosahedron(pts1, pts2, pts3)
tList = iCos[0]
mesh = iCos[1]

#subdivide each face of icosahedron into triangles recursively
allTrianglePts = []
allTrianglePts = subTriPtRecurOnPrimary(tList, recur, allTrianglePts)
#get flattened list triangles on each face if desired for display
flatPolyLineList = displayPrimaryTrianglePts(allTrianglePts)
#project all triangles on each face away from center according to value of the radius
projAllTPoints = projectPts(allTrianglePts, ctrPt, radius)
#build surface of icosahedron as well as face centerpoints and face normals
surfData = buildPolysurf(projAllTPoints, ctrPt)

#display of primary geometry and output of facet centerpoint normals
if(displayGeodesic):
    m = surfData[0] #mesh surface (combined icosahedron faces)
    c = surfData[1] #mesh face centerPts (icosahedron face centerPts)
    n = surfData[2] #mesh face normals (icosahedron face normal vectors)

#display of secondary interim construction element geometry (if desired)
if (displayCE):
    i = mesh # primary icosahedron at radius 1
    g = mesh1, mesh2, mesh3 #golden rectangles
    t = flatPolyLineList #flat triangles on each face of primary icosahedron

#print the number of faces = number of face normals
print("Number faces " + str(len(n)))

Summary

Within this workshop we have developed a few basic scripts for representing three-dimensional surfaces . The principal building block of these surface elements has been a three sided triangular polygon. We examined how such three sided polygons could be spherically projected so as to create various kinds of geodesic surfaces. The examples also demonstrate the power of  vector methods of projection where we follow a three step process:

1. Find the vector from the center of the surfacefor each vertices on a triangulated surface.
2. Change each such vector into one of unit length 1.0  (a so-called "unit" vector)  but having the same direction as the original vector.
3. Scale each vector by the radius value to get the triangulated points of the surface desired.

This is a not untypical approach to working through the use of vectors in geometrical modeling.