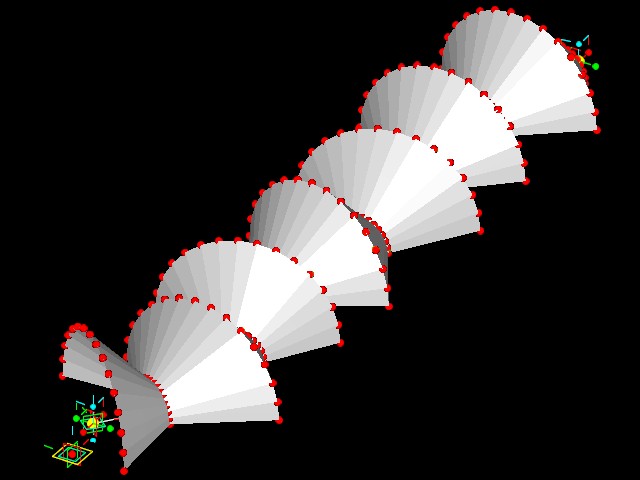
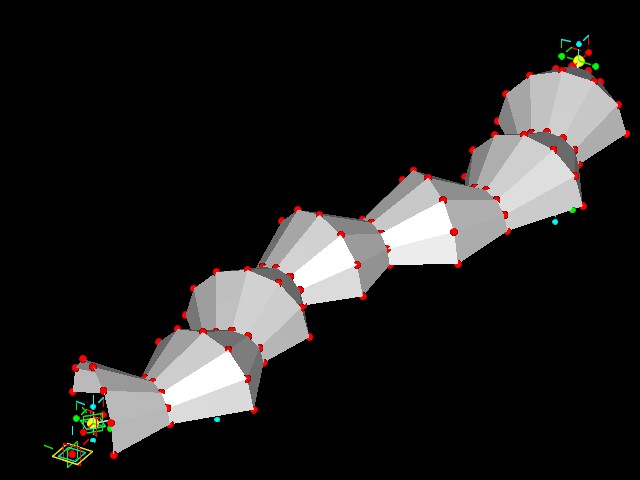
Workshop 10 notes, Week of November 5, 2007

GENERATIVE COMPONENTS WITH FUNCTIONS EXAMINED

General Background

It is possible to encode a step-by-step form generating process using a language that more abstractly may express a designer's intentions.  Expressions of this kind include performing a set of tasks repeatedly  until a certain condition is satisfied.  For example, a tower may rotate from floor to floor until the top floor of a building is reaced.  Or, a specific construction may be performed when some condition is met.  For example, a set of shading louvres may be open conditional upon the desire for solar gain. In this extension of parametrically determined geometry, we use constructions in a simple language to describe desirable formal outcomes. 

With Generative Components it is possible to include such abstract expressions as a part of a form generating procedure. Within the workshop this week, we explore a number of related examples.

Examples of Geometrically Progressive Forms 
(Source: Harvard Design Magazine, Spring/Summer 2007, Number 26. Calatrava project from inside front cover, FOA and SOM projects from Alejandro Zaera-Polo, "High-Rise Phylum 20007".)

Santiago Calatrava . Fordam Tower, Chicago, 2005, Twisting Tower, Curved Sides, Reducing Radius

FOA Bundle Tower, New York City, 2001,Grid adjusts to Curve

SOM, Burg Dubai flower-like plan form after Hymenocallis flower (Dubai), direct transplant of organic forms.

Abstract Language of Procedures

Procedure: A series of steps for  performing a task.

EXAMPLE 1 Toast Espresso

from Richard Purdie (RPURDIE@clear.co.nz)

Toaster Crumbs
Water

1- empty all the delicious crumbs out of the bottom of the toaster.
2- place in the coffee perk or cappucino Machine
3- process as per coffee.
4- adjust to suit your taste. 

Modified Procedure using two constructions, an "if" statement and a  "for" loop.

EXAMPLE 2 Toast Espresso2 WITH "IF" and "WHILE" statements

Toaster Crumbs
Water

1- empty all the delicious crumbs out of the bottom of the toaster.

    IF ( TOASTER  != EMPTY) THEN

        REMOVE TOAST AND TILT TOASTER FOR CRUMBS

    ELSE

        TILT TOASTER FOR CRUMBS

     END IF

2- place in the coffee perk or cappucino Machine
3- process as per coffee.
4- adjust to suit your taste. 

    WHILE (COFFEE < FULL_TEXTURE) {

            ADD TWO CRUMBS

   }

---

Example 3 ARCHIMEDES SPIRAL IN GC

We begin with some variables:

double angularincrement = 5;  //The distance between angular rotations of radial points
double numrevolutions =  4;  //number of revolutions of the spiral
double radius = 5; // initial radius of spiral
radialincrement = 0.1; //increase in redius with each new radial point
radaccel = 1; //accelaration of radius per new radial point (i.e., 1 causes no acceleration, 1.01 causes acceleration)

Now we write a function to create the spiral:

function (CoordinateSystem cs, double numrevolutions, double angularincrement, double radius, double radialincrement, double radaccel)
    {
   
    Point curvePoints = {}; //create a list for holding points
   
    double curdegree = 0; //set the degrees to 0 for starting the curve
    int i = 0; //set the value of this counter to zero
    double xval, yval, zval; //create cartesian coordinate variables
   
    while (curdegree < (numrevolutions * 360))
    {
    // build the points for the curve
        xval = Cos(curdegree) * radius;
        yval = Sin(curdegree) * radius;
        zval = 0;
        Point curPoint = new Point(this); //create a point holder
        curPoint.ByCartesianCoordinates(cs, xval, yval, zval);
        curvePoints[i] = curPoint;
        i = i + 1;
        radius = (radius + radialincrement) * radaccel;
        curdegree = curdegree + angularincrement;
    }
    // create the polygon determined by the points
        PolyLine p1 = new PolyLine(this);
        p1.ByVertices(curvePoints);
    }

We could add a variable for height increment, such as "float heightincr = 0.01" and the spiral would move upward as it radiates outward. Here, we would change the statement above "zval = 0;" to "zval = zval + heightincr;"

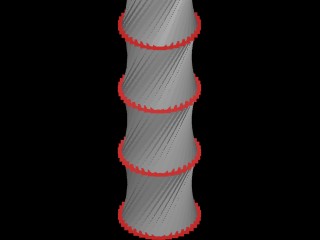
Spiral generated for default values:



Increase angular increment between points from 5 to 7. Spiral shrinks but distance between points is creater.


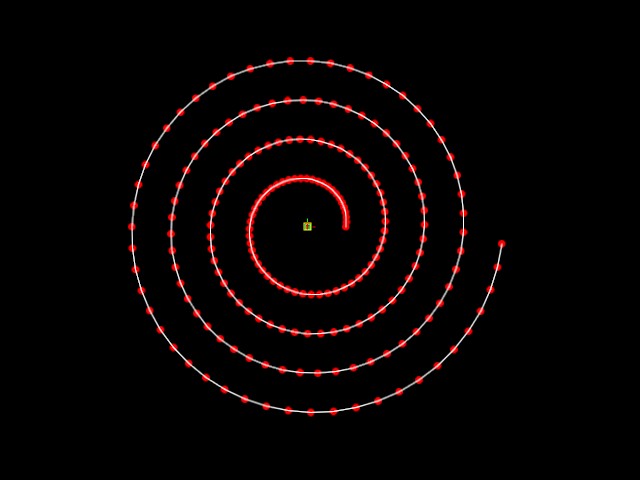
Increase acceleration from 1.0 to 1.1 and we get a logarithmic curve quickly accerating outward (next two images show a) same scale as one above, and b) full curve.


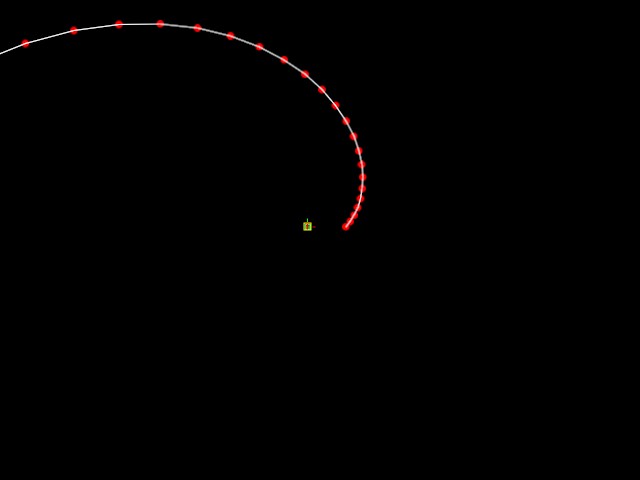
same scale

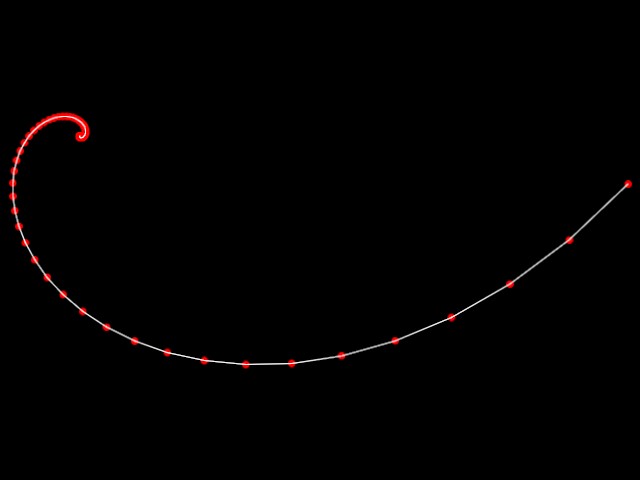
full curve


Now we slow down acceleration to 1.02 and we see more of geometry of curve.

---

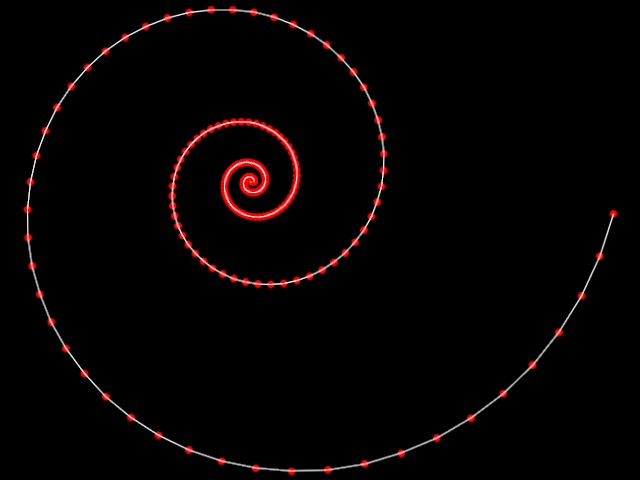
Example 4 VENTIAN BLINDS WITH SOLAR SHADING CONTROL

The objective is to build a shading device that is varied according to the angles of the sun.

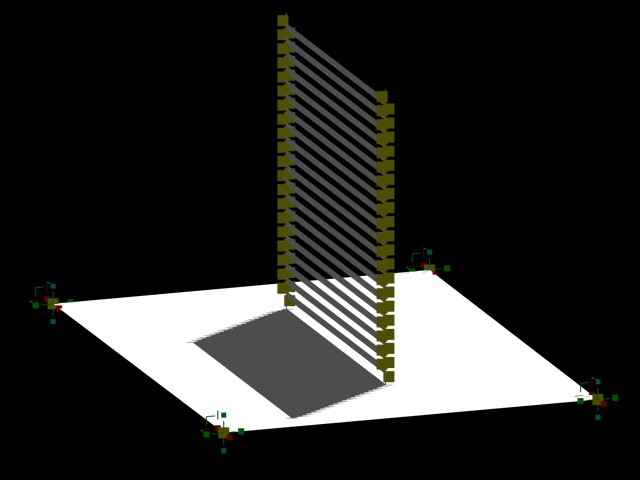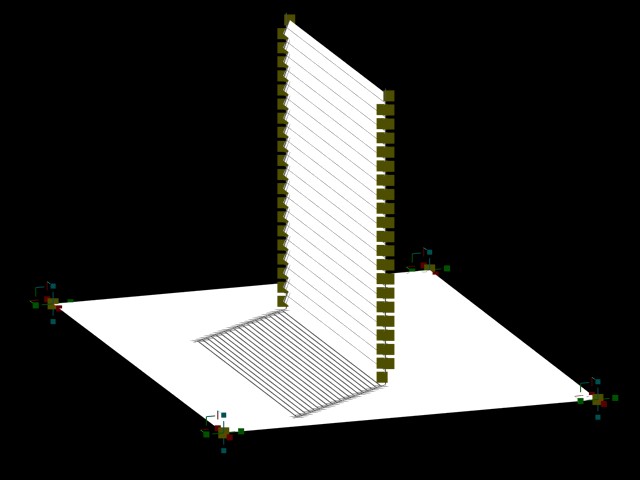Shading scenario	DIrect solar gain scenario

We begin with some variables:

sunangle = 48; //angle of the sun (altitude based on latitude and longitude and time of year)
shading = 1; //set to 1 when shading, and -1 when not
blindangle = sunangle * shading;  //angle of shading blinds which is based on sunangle *shading
depth = 0.5; //depth each blind
numblinds = 20; //number of blinds in whole shading device
width = 10; //width of of entire shading device
windowheight = 10; //height of entire shading device

STEP 1:

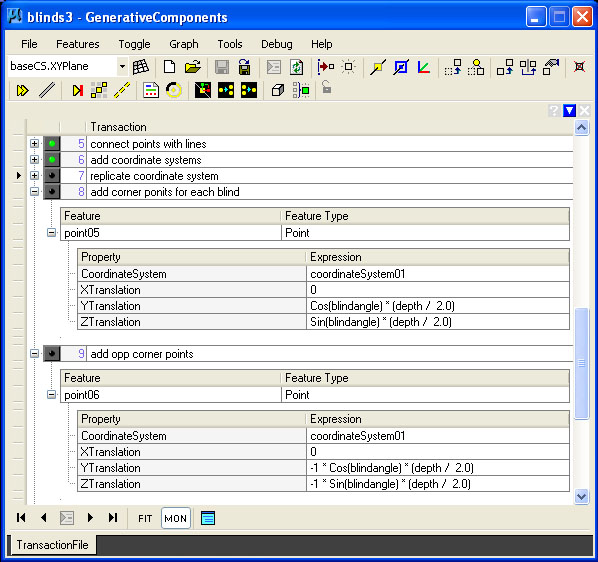
The key function for controlling the blinds is developed as follows using similar logic as the spiral. We place an auxiliary coordinate system at each end of every blind.



STEP 2:

We define points in the YZ plane of the coordinate system according to the following specification of x, y and z coordinates:

STEP 3:

These coordinates are in turn used to define the polygons of each blind.

To create the polygons, a function is used with a for loop, were point1 and point2 are lists of the front and back points for all the blinds. Pont1 lists the front corner points of all the blinds in an indexing system where point1[0] containts the front two corner points of the first blind, and point1[1] contains the front  two corner points of the second blind. Note that this is a zero based (e.g., "0") indexing system, where 0 is the index for the first set of front corner points, 1 is the index for the second set of front corner points, etc.,  Going further, point[0][0] is the first of two front corner points in the first blind, and point[0][1] is the second of two front corner poits of the first blind.

function (Point point1, Point point2, int numblinds) {  //function takes two points with coordinates of front and back of blinds

Point curVertices = {}; //creates an empty list of points
for (int i = 0; i <= (numblinds + 1); i++)  //initializes i at 0, proceeds until i = number of blinds - 1, increments i by 1 each loop
{
    curVertices[0] = point1[i][0]; //gets first endpoint in point1 for blind  number "i"
    curVertices[1] = point1[i][1]; //gets second endpoint in point1 for blind  number "i"
    curVertices[2] = point2[i][1]; //gets first endpoint in point1 for blind  number "i"
    curVertices[3] = point2[i][0]; //gets second endpoint in point1 for blind  number "i"
    
  Polygon curPoly = new Polygon(this);  //creates polygon for the blind number  "i"
  curPoly.ByVertices(curVertices);
   
}
}

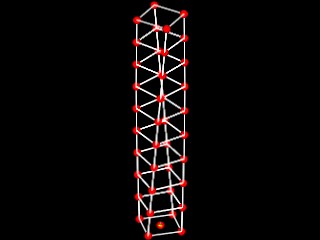
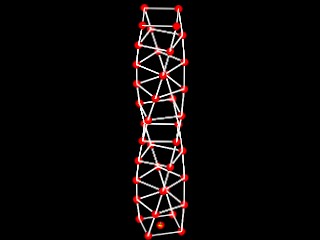
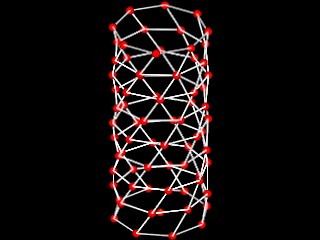
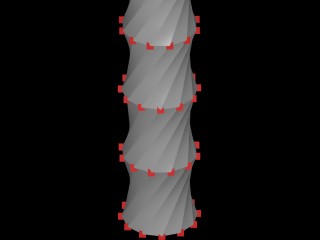
Example 4 TWISTING TOWER WITH VARIABLE NUMBER OF CORNERS

This example furthers the case study of the twisting tower from last week, and uses the same variables. The key to making this generative component more flexible is the use of the following function below, where

incolangleincrement = floor to floor twist in rotation
sPnum = number of corner points
height = height of each floor
num = number of floors


function (CoordinateSystem cs, double incolangleincrement, int num, double height, int spNum, double radius)

{
Point points = {};
for (int j = 0; j < spNum; ++j) //outer loop for each corner of tower

{
    double xPosSeries = {}; //create a series for each set of corner points
    double yPosSeries = {};
    double zPosSeries = {};
   
    for (int i = 0; i < num; ++i)  //inner  loop for each point  given corner of tower

        {

            double shift = 360/spNum*j; //rotate to new corner each time through loop.
            double xPos = Cos((incolangleincrement*i) + shift)*radius;  //calc. x, y, z values for each corner point.
            double yPos = Sin((incolangleincrement*i) + shift)*radius;
            double zPos = height/num*i;
           
            xPosSeries[i] = xPos;
            yPosSeries[i] = yPos;
            zPosSeries[i] = zPos;
        }
           
            Point pointcur = new Point(this);  //create the set of  points from vertice for  given corner of tower
            pointcur.ByCartesianCoordinates(cs, xPosSeries, yPosSeries, zPosSeries );
             points[j] = pointcur;

        
       
       if (j > 0) {  //if beyond first corner, create polygon for this corner and preceding corner
          Polygon skinpoly = new Polygon(this);
          skinpoly.ByLacing(points[j],points[j-1]);
          }
        if (j == (spNum - 1)) { //if at last corner, create polygon for this corner and fist corner
          Polygon skinpoly = new Polygon(this);
          skinpoly.ByLacing(points[j],points[0]);
        }

    }
    
 }

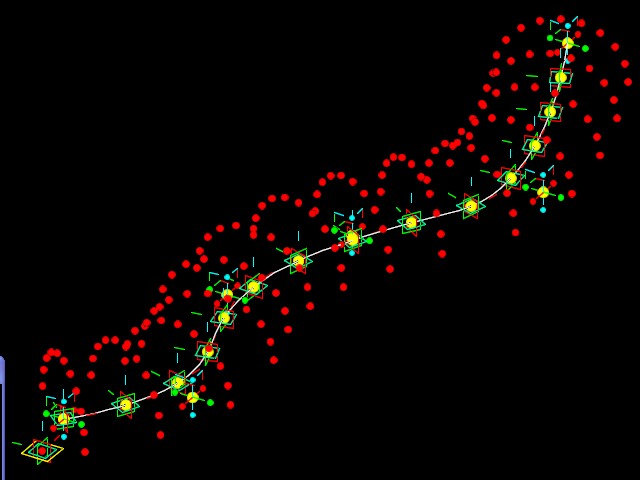
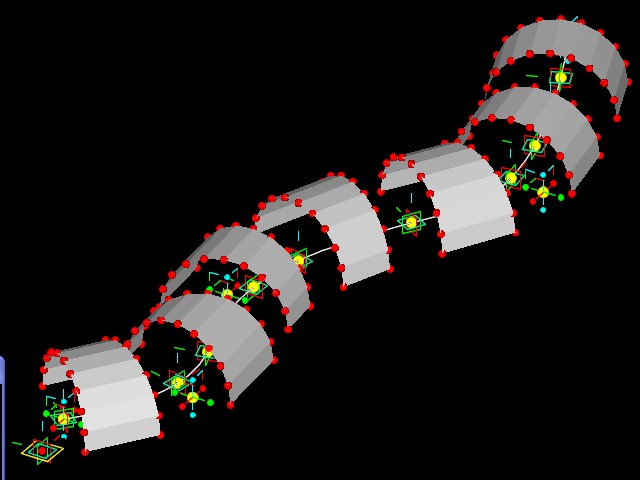
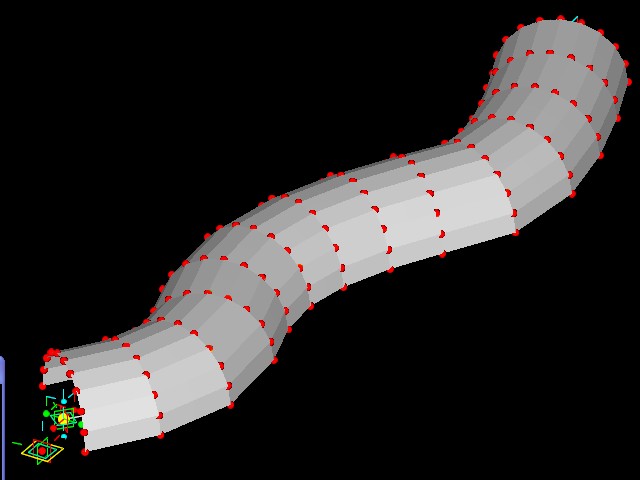
Example 5 TWISTING ARCHES OF ALERNATING RADIUS FOLLOWING A BSPLINE