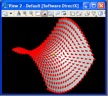
CAAD: GENERATIVE COMPONENTS & PROCESS BASED DESCRIPTION
PART II:
Generative Components (GC)
Vectors and Functions Revisited in Detail
We review five examples of GC scripts. All the script files may be downloaded by selecting the links given below. The last four examples are developed with the use of "ByFunction" update methods. The "ByFunction" methods can accommodate some very efficient techniques and express algorithmic logic.
EXAMPLE 1. Hyperbolic parabolic surface by means of a basic scripting technique
We begin by establishing a point grid on the ground plane. We then use the equation of a hyerbolic parabolic surface to establish a point at a vector distance from each point on the ground plane. The full script is hyperbolicparabolicbyhand.gct.

Step 1: Create vars for resolution (e.g, 1.0) and scale (e.g., 0.2).
Step 2: Use Create feature tool create point01 via two Series expressions as described in the table below.
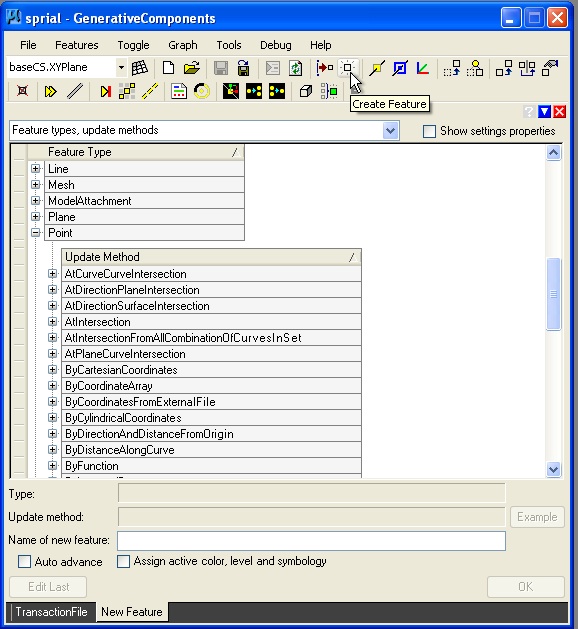
Using the ByCartesianCoordinates update method, we enter the following values.
| Point01 | |
| CoordinateSystem | baseCS |
| XTranslation | Series(-10,10,resolution) |
| YTranslation | Series(-10,10, resolution) |
| ZTranslation | 0 |
Step 3: Replicate the point
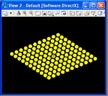
Step 4: Add a point02 at a vector direction (Zdirection) and distance (hyperbolic parabolic equation) from point01
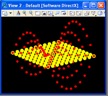
| Origin | point01 |
| Direction | baseCS.Zdirection |
| DistancefromOrigin | scale * ((point01.x * point01.x) – (point01.y * point01.y)) |
Step 5: Hide base points
Step 6: Create polygon mesh from point02
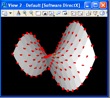
EXAMPLE 2: Simple Graphics Function
A graphics function can provide a more efficient way to realize a GC script and may allow for embedded logic that ties closely to the intentions of a process. A simple example is that of a drawing a given point. The full script is mypoint.gct. The script creates the point in the upper right-hand corner of the window below.
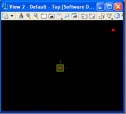
Step 1: Setup graphic variables for the xvalue, yvalue and zvalue of the point.
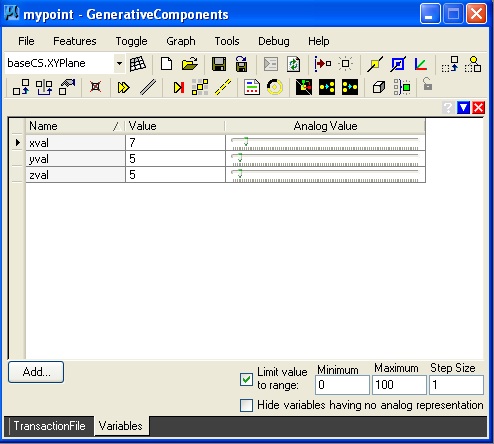
Step 2: Create a point feature using the "byFunction" update method.
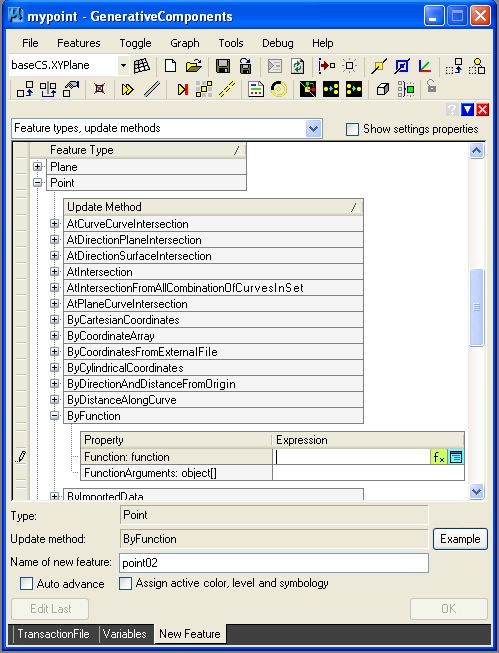
Using the editing box at the right hand side of the function entry text area, enter in the following text:
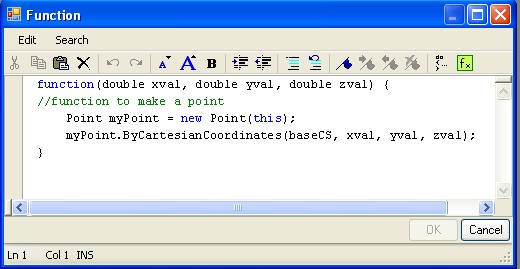
function(double xval, double yval, double zval) {
//function to make a point
Point myPoint = new Point(this);
myPoint.ByCartesianCoordinates(baseCS, xval, yval, zval);
}
Within the editor, the text appears as follows:
NOTE:
1. There are three "arguments" to the function, xval, yval and zval, each a double (decimal) number.
2. Comment lines are preceded by // and appear in the color green. They are not executed in the script but exist for documentation.
3. Declare an object point with Point myPoint = new Point(this); - the word ”this” makes the point visible on screen
4. myPoint.XXX - the dot "." operator is used to access procedures available to the myPoint object
5. myPoint.ByCartesianCoordinates(baseCS, xval, yval, zval); - the ByCartesianCoordinates update method is selected
6. variables for xval, yval and zval are pased as a list are also enclosed in curly brackets in the second line {xval, yval, zval} (see below)
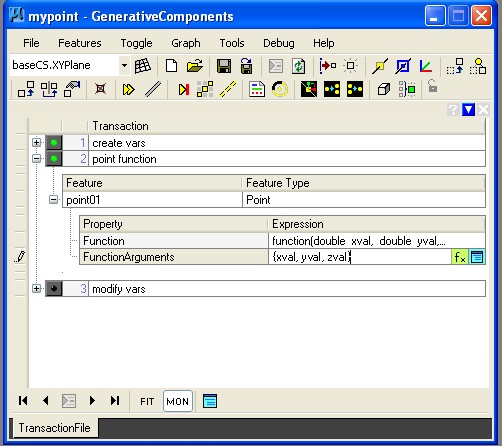
The symbolic graph shows the relationship between the variables xval, yval, and zval, and the point point01.

EXAMPLE 3: Spiral Function
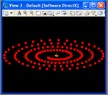
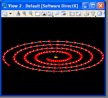
The spiral function uses a "while" loop to iterate through a series of points spiraling outwardly from the origin. The full script is sprial.gct.
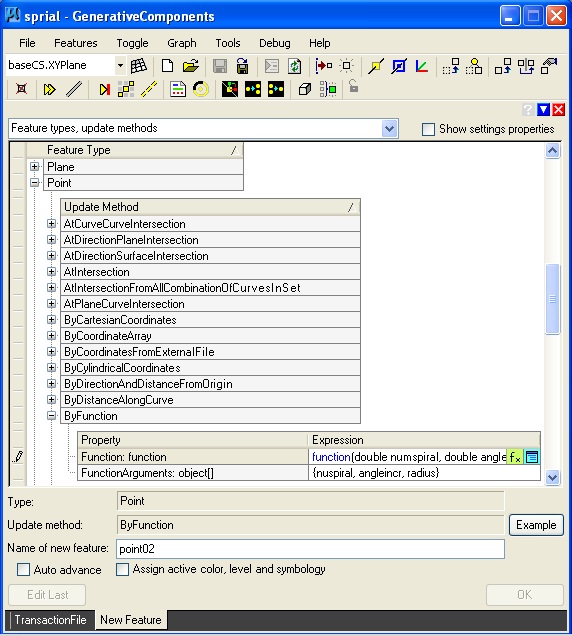
Step 1: Create vars for numspiral, angleincr
and radius
Step 2: Use create feature tool to ceate a point by the "ByFunction" update method.
Start with the "Create Feature" tool.

Use the "ByFunction" update method.
function (double numspiral, double angleincr, double radius) {
// function to draw an archimedes curve
double xval, yval, zval; //declare variables internal to function
double curangle = 0;
double radincr = radius / (360 / angleincr);
while (curangle < (numspiral * 360)) //START LOOP
{
Point curPoint = new Point(this); //initiate new point
xval = Cos(curangle) * radius;
yval = Sin(curangle) * radius;
zval = 0;
curPoint.ByCartesianCoordinates(baseCS, xval, yval, zval); //make point at given values
curangle = curangle + angleincr; //advance angle of point relative to origin
radius = radius + radincr; //increase size of radius
} //END LOOP
} //END FUNCTION
Step 3: Add polyline to points by using the "ByVertices" update method.
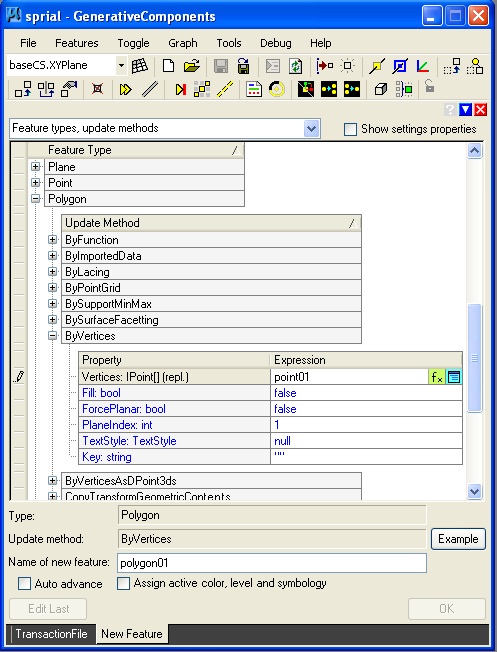
The sprialing points are then connected with a polygon line as suggested in the following image.
EXAMPLE 4: Hyperbolic Parabolic Surface with Polygon Function (avoid intermediate ground plane points of example 1).
The full script is hyperbolicparabolic.gct.
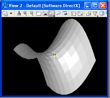
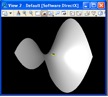
Two different resolutions
Step 1: Create vars for resolution, size and scale.
Step 2: Use the create feature tool to create a polygon surface using a ByFunction update method
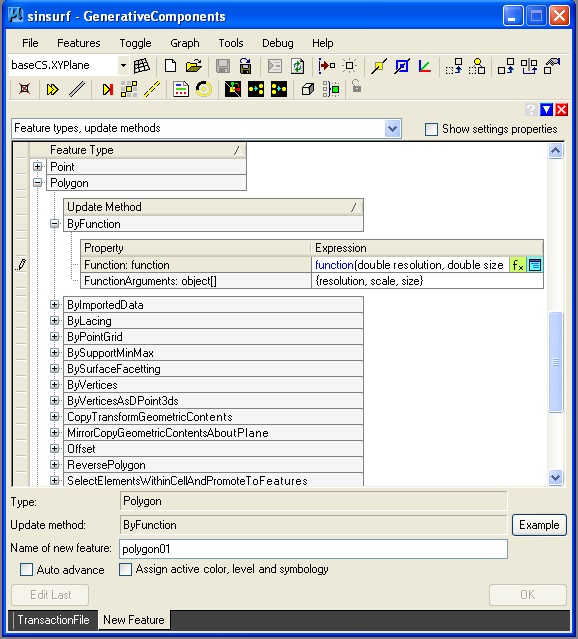
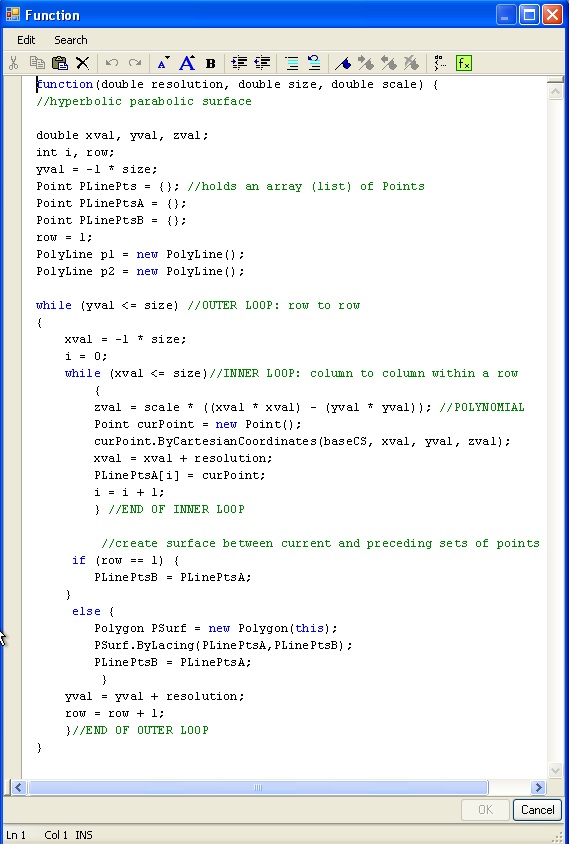
function(double resolution, double size, double scale) {
//hyperbolic parabolic surface
double xval, yval, zval;
int i, row;
yval = -1 * size;
Point PLinePtsA = { };//holds an array (list) of Points
Point PLinePtsB = { };
row = 1;
PolyLine p1 = new PolyLine();
PolyLine p2 = new PolyLine();
while (yval <= size) //OUTER LOOP: row to row
{
xval = -1 * size;
i = 0; //index into array of points
while (xval <= size) //INNER LOOP: column to column within a row
{
zval = scale * ((xval * xval) - (yval * yval)); //KEY POLYNOMIAL EQUATION
Point curPoint = new Point();
curPoint.ByCartesianCoordinates(baseCS,
xval, yval, zval);
PLinePtsA[i] = curPoint;
//store point in array of points
i = i + 1;
//advance index for array of points
xval = xval + resolution;
} //END OF INNER LOOP
//create polygon surface between current and preceding sets of points
if (row == 1) {
PLinePtsB = PLinePtsA;
}
else {
Polygon PSurf = new Polygon(this);
PSurf.ByLacing(PLinePtsA,PLinePtsB); //laces two rows of points into polygon
PLinePtsB = PLinePtsA;
}
yval = yval + resolution;
row = row + 1;
}//END OF OUTER LOOP
}
Inside the editor, the code would appear as follows:
Example 5: Sin Points with Polygon Surface
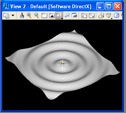
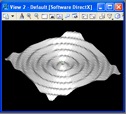
Two different frequencies
The full script is sinsurf.gct.
Step 1: Create vars for frequency, resolution, size and scale.
Step 2: Use create feature tool to create polygon surface function.
function(double resolution, double size, double scale, double frequency) {
//sin surface function
double xval, yval, zval;
int i, row;
yval = -1 * size;
Point PLinePtsA = { };//holds an array (list) of Points
Point PLinePtsB = { };
row = 1;
PolyLine p1 = new PolyLine();
PolyLine p2 = new PolyLine();
while (yval <= size) //OUTER LOOP: row to row
{
xval = -1 * size;
i = 0;
while (xval <= size)//INNER LOOP: column to column within a row
{
zval =
scale * Sin(frequency * Sqrt((xval * xval) + (yval * yval))); //KEY POLYNOMIAL EQUATION
Point curPoint = new Point();
curPoint.ByCartesianCoordinates(baseCS, xval, yval, zval);
xval = xval + resolution;
PLinePtsA[i] = curPoint;
i = i + 1;
//advance index for array of points
} //END OF INNER LOOP
//create polygon surface between current and preceding sets of points
if (row == 1) {
PLinePtsB = PLinePtsA;
}
else {
Polygon PSurf = new Polygon(this);
PSurf.ByLacing(PLinePtsA,PLinePtsB);
//laces two rows of points into polygon
PLinePtsB = PLinePtsA;
}
yval = yval + resolution;
row = row + 1;
}//END OF OUTER LOOP
}