The primary focus of this workshop notes are conditional statements and iteration to produce an array of figures n 2D. As we will see in the workshop that follows this one, similar techniques can be used to produce 3D arrays on various surfaces defined by polynomial expressions.
Also, these notes continue the use of function definitions inside of Python within Grasshopper . They introduce "if else" conditional expressions. In addition, they introduce the "for i in range" type expressions.
For detailed references on the avaialble libraries used in the examples below see:
Rhino
Common Libary - functions for Rhino Python, most of
which are alsoavailble to the Python scripting component within Grasshopper.
Rhino Script Syntax Library - functions for Rhino Python, most of
which are also availble to the Python scripting component within Grasshopper.
For published tutorials and manuals see:
Python
Scripting for Rhino and Grasshopper - overview
The
RhinoPython 101 manual. - step by step tutorials pdf file
primer
1. Simple Polygon Array Function
This first example demonstrates the construction of an array of rectangles in 2D space with rows in the "y" axis, where each row consists of a column of figures in the "x" axis direction.
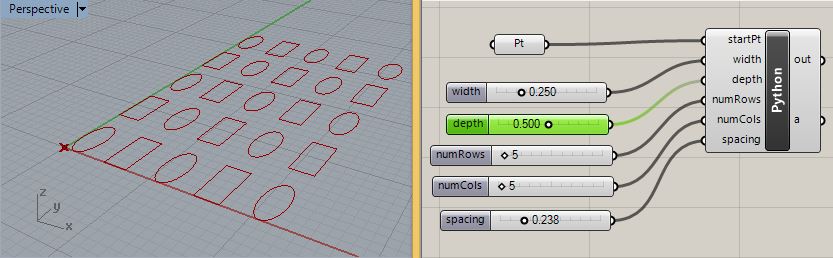
1a. Initiate the procedure by setting up a 3D point and numerical slider parameters:
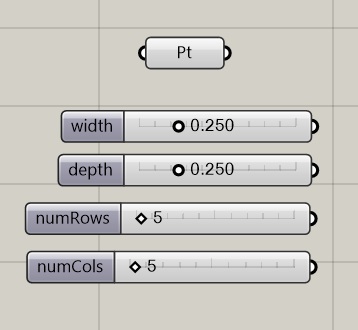
Set the value range of width and depth from 0.0 to 1.0 as floating point numbers, where width and depth determine the size of each rectangle.
Set the value range of numRows and numCols from 2 to 100 as integer numbers, where they determine the number of rows and columns within the array.
1b. Connect the point to a corresponding point in Rhino and prepare input parameters to an Python scripting compenent inside Grasshopper.
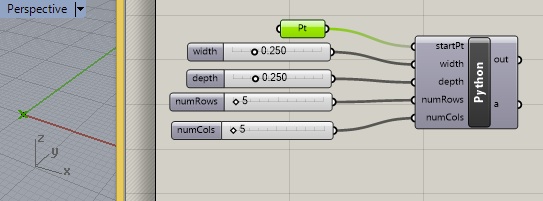
1c. Import the Rhino and Rhinoscript libraries into the Python component and begin developing the script by writing a function "def drawRect(originPt, w, d)" that draws a rectangle from a an "originPt" on its lower-left corner for a given "w" (width) and "h" (height). Note that these variables have a "scope" that is local to this function (see 1d. below).
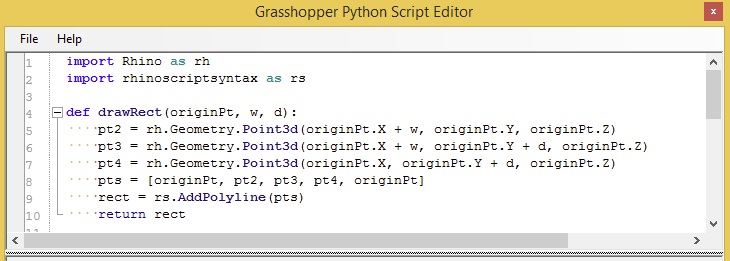
1d. Test the function by setting up the output variable "a" to be equal to the return value of drawRect. Note that the use of variables "startPt", "width" and "depth" are spelled exactly the same as the input parameters to the Python script. They can be spelled differently than the local variables "originPt", "w" and "d" in 1a. above. That is, the values of "startPt", "width" and "depth" and passed on the variables "originPt", w" and "d"in the procedure "drawRect".

1e. Now add a function "def drawArray(originPt, w, d, nRow, nCol)" to place the rectangles in an array, where "originPt" is the lower-left hand point in the array, and where "nRow" and "nCol" are variables that represent the number of rows and number of columns respectively, and where "w" and "d" represent the width and depth of each individual rectangle. Set the output variable "a" to the result of the "drawArray" function to visualize the results in Rhino.
Note that the function contains an outer loop based upon an index variable ii. Inside of the outer loop is nested and inner loop based upon an index variable "ii". The statement "for ii in range(0, nRow, 1)" initiates the outer loop. The initiates the value of ii as "0" during the first time through the loop, and continues to repeat the loop while the value is less than or equal to nRow. The value of "ii' is incremented by 1 each time through the loop. As used in line 16 of the function, the value of "ii" it steps row by row from the origin of the coordinate system and up the postivie "y" axis. This is because it used to set the "y" coordinate of each "originPt "of each rectangle. Similarly, for any given row, the statement "for i in range(0, nCol, 1)" initiates the inner loop. As used in line 16 of the function, the value of "i" steps column by column from the origin of the coordinate system to the right along the positive "x" axis by determing the "x" coordinate of each "originPt". More generally, the range function has the form:
"for index_variable in range(start_value, end_value, increment_value):"
The lines of the Python script indended after line 14 are repeated until the index variable ii > nRow.
2. Adding A Space Parameter.
A new input slider variable "space" can be used to adjust the spacing between the rows and columns of rectangles. First note that the slider, a floating point number with the range of 0.0 to 1.0, is added to the input parameters to produce rectangles spaced at a specified distance (e.g. "0.200") apart in the rows and columns.
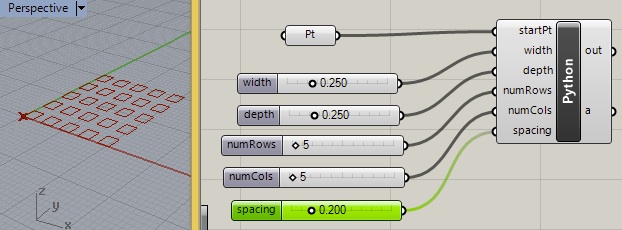
Next, the input parameter "spacing" is added to the drawArray function. Note that in line 22 below, the parameter "spacing" is the fourth parameter in the function call. Correspondingly, in line 12 below, the parameter "s" is the fourth parameter used in the "Def" statement. The implmentation of the spacing is then comleted in line 16 below, where the x and y coordinates of each rectangle's "originPt" are adjusted correspondingly by the values of "i * (w + s)" and "ii * (d + s)".
3. Using Logical "and" and "or".
To vary the pattern a logical "and" ora logical "or" or both can can be used to setup alternating figures between rows and columns.
3a. For example, in the modification below, the function "def drawEllipse" is added to the script with the same input parameters as "def drawRect". Line 13 within the function determines a vector "vec1" normal to the x-y plane. For the "originPt" input parameter for any given ellipse, line 14 creates its "centerPt" displaced at a distance of 1/2 the width and 1/2 the height. Next, line 15 uses a Rhino library ('rh") function to create a construction "plane" based upon the "centerPt" and "vec1". In turn, line 16, creates the ellipse "el" centered at the origin the "plane" with radius values of w/2.0 and d/2.0. Note that the division by 2.0 ensures that w/2.0 and d/2.0 returns a floating point number for accuracy rather than a more approximate integer number. Tha is, dividing a floating point number by a floating point number returns a floating point number, but dividing a floating point number by an integer truncates the result to an integer.
3b. Once the "def drawEllipse" function is completed, then it can be incorporated in the the drawArray function into a conditional "if else" statement as indicated in lines 25 through 36 below. In particular, if "i == ii" (the number of the row is equal to the number of the column") then draw a rectangle. "Else" (otherwise) draw an ellipse. The resulting objects, whether a rectangle or an ellipse are returned from the function through the array "objList.
3c. Finally, the call to the function in line 32 isn't changed and the entire script appears as follows.
The resulting array appears as follows:
3d. An alternative variation of the "if else" statement uses a combination of "and" and "or" expressions in line 24 below.
This one change to the "if else" clause results in the new pattern below.
3e. Note that adjusting the slide for "depth" results in changes to the proportions of the ellipses and the rectangles.
For a closer understanding of the "if else" statement in line 24, see part 4 below.
4. The Precedence Rules for Logical Operators Or and And
We have introduced conditional statements and logical operators "or" and "and", and in the last example a relatively complex combination of these operators within nested parenthes. We now need to go into greater detail regariding the precedent rules that impact how to Python statements in which they have appeared. We we can summarize the precedent rules regarding "or" and "and" operators as we;; as other mathematical operators as follows:
| ( ) | Parenthesis |
| or | Logical OR Operator |
| and | Logical AND Operator |
| pow | Exponentiation |
| - | Unary minus with one argument, e.g., -3 |
| *, / | Multiplication, Division |
| % | Modulo |
| +, - | Addition, Subtraction |
A few examples below give
further evidence as to how the computer evaluation procedure works for the Or and And operators. Within each example, the initial line is replaced
by a new line where the rules of evaluation have been applied in the correct
order.
First note that following statement is true if and only if both the expression1 and expression2 are true:
expression1 and expression2
Also, not that the following statement is true if either the left expression1 is true or the right expression2 is true:
expression1 or expression2
a = 3
b = 6
if (a == b or a > b):
....
-> The "or" operator has precedence and we evaluate the expressions to its
left side first
-> The first expression evaluates to 3 == b
-> The first expression evaluates to 3 == 6
-> The first expression evaluates to not true
-> the expression to the right of the OR operator a > b is
evaluated
-> The second expression evaluates to 3 > b
-> The second expression evaluates to 3 > 6
-> The second expression evaluates not true
-> the OR operator is applied to the expressions on its left and
right
-> the whole statement is not true
a = 3
b = 6
if (a > b or b == 2 * a ):
....
-> The "or" operator has precedence and we evaluate the expression to its left
side first
-> The first expression a > b evaluates to 3 > b
-> The first expression a > b evaluates to 3 > 6
-> The first expression evaluates to not true
-> the expression to the right of the OR operator b = 2 * a is evaluated
-> The second expression evaluates to 6 == 2 * b
-> The second expression evaluates to 6 == 2 * 3
-> The second expression evaluates to 6 == 6
-> The second expression evaluates to true
-> the OR operator is applied to the expressions on its left and
right
-> the whole statement is true
a == 3
b == 6
if (b == 2 * a and a == b):
....
-> The "and" operator has precedence and we evaluate the expression b == 2 *
a to its left side first
> The second expression evaluates to 6 == 2 * a
-> The second expression evaluates to 6 == 2 * 3
-> The second expression evaluates to 6 == 6
-> The second expression evaluates to true
-> the expression to the right of the AND operator a == b is
evaluated
-> The second expression evaluates to 3 == b
-> The second expression evaluates to 3 == 6
-> The second expression is not true
-> the AND operator is applied to the expressions on its left and
right
-> the whole statement is not true
a = 3
b = 6
if (b > a and b < 2 * a or b == 2 * a):
....
-> The "or" operator has precedence and we evaluate its left side first
-> The "and" operator has next precedence and we evaluate its left side first
-> The first expression b> a evaluates to 6 > a
-> The first expression b> a evaluates to 6 > 3
-> The first expression evaluates to true
-> the expression to the right of the "and" operator b < 2
* a is evaluated
-> The second expression evaluates to 6 < 2 * b
-> The second expression evaluates to 6 < 2 * 3
-> The second expression evaluates to 6 < 6
-> The second expression evaluates to not true
-> the "and" statement evaluates to not true
-> the expression to the right of the "or" operator b == 2 * a is evaluated
-> The expression to the right of the"or" operator evaluates to 6
== 2 * a
-> The expression to the right of the"or" operator evaluates to 6
== 2 * 3
-> The expression to the right of the"or" operator evaluates to 6
== 6
-> The expression to the right of the"or" operator evaluates to true
-> the OR operator is applied to the expressions on its left and
right
-> the whole statement is true
Note that parenthesis ( ) can be used to override the normal operator precedence.
We can apply parenthesis to the previous examples,and we change the results
of the computer evaluations. You might convince yourself that the first of the
following two examples evaluates to true whereas the second evaluates
to not true:
a = 3
b = 6
if (b = 6 or b < a and b = 2):
....
a = 3
b = 6
if (b = 6 | b < a) & b = 2):
....
Now we evaluate the if stateemnt used in 3d. above.
For the 3rd row and first column of the array of squares and ellipses we have:
ii = 2
i = 0
....
if ((i % 2) == 1) and ((ii % 2) == 0) or ((i % 2) == 0) and ((ii % 2) == 1):
....
> The "or" operator has precedence and we evaluate its left side first
> The "and" operator has next precedence and we evaluate its left side first
-> The first expression to the left of the "and" operator is (i % 2) == 1 and evaluates to 0 == 1
-> Therefore, the first expression to the left of the "and" operator evaluates to "not true"
-> Therefore, the "and" operator evaluates to "not true" since the left side of the "and" expression is not true
-> Since the last step implies that left side of the "or" statment is "not true" then it is necessary to see if the right side of the "or" statement is true
-> The "and" operator has next precedence and we evaluate its left side first
-> The first expression to the left of the "and" operator is (i % 2) == 0 and evaluates to 0 == 0
-> Since the last step implies that left side of the "and" statment is " true" then it is necessary to see if the right side of the "and" statement is true
-> The first expression to the right of the "and" operator is (ii % 2) == 1 and evaluates to 0 == 1
-> Since the last step implies that right side of the "and" statment is "false" then the right side of the "or" statement is false
-> Since the both the left of the "or" statement is false and the right side of the "or" statement is false then the entire statement is false
Since the statement is false, then for the thrd row and first column the result is that the "else" clause in the example of 3d is invoked,