COMPUTER AIDED ARCHITECTURAL DESIGN
Workshop 16 Notes, Week of November 11 , 2018

SURFACES BASED UPON POLYNOMIAL EXPRESSIONS

In the examples below, polygons are described with reference to the World Coordinate System. It is an eclectic collection derived from various textbook sources; however, there is consistency in how the basic surface elements are generated. In the examples polynomial expressions are used to calculate the vertices of a number of simple four sided surface polygons. The four sided surface polygons are juxtaposed in three dimensional space so as to create larger surface areas. 

PART 1. Hyperbolic Parabolic Surface Points

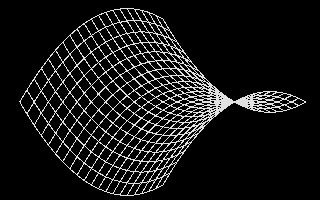
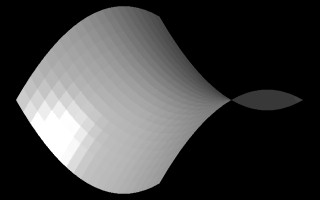
In the illustration in the figure  below, we see a polygonal mesh description of a hyperbolic paraboloid shape on the left-hand side and its rendered surface description on the right-hand side [derived from Lord, The Mathematical Description of Shape and Form, John Wiley and Sons, 1984].

Perspective View Hyperbolic Parabolic surface

The x-coordinate and y-coordinate of the polygon vertices range over a set of values stepping in increments of 0.1  from -1  to +1. That is, we have -1 <= Point.X <= 1 and -1 <= Point.Y <= 1. Note the regularity of this uniform x-coordinate and y-coordinate grid mesh is apparent when seen in the plan view as depicted below. However, the z-coordinate changes non-uniformly from vertex to vertex and accounts most directly for the curvature that is apparent in the views of the surfaces above.

Plan View Hyperbolic Parabolic surface

Sub procedure that calculates the z-coordinate of the hyperbolic paraboloid surface

The full Python script  that generates the hyperbolic paraboloid surface will be given further below. First, however, we examine the logic of some of its parts. For each of the four sided polygons above, the z-coordinate value of each vertex is the function of its x-coordinate and y-coordinate values. The general mathematical expression used to calculate the z-coordinate of the vertices is:

where s is a scalar coordinate, z is the z-coordinate, x is the x-coordinate, and y is the y-coordinate value of a particular given polygon vertex in the figure above, and where "pow" exponentiation function.  Note that to generate the specific surface above, cScalar = 0.1, -10 <= x < 10, and -10 <= y <= 10. Modification of the scalar s impacts the relative height the z-coordinate each polygon vertex:

In particular, examine an expression that takes a three dimensional Point and calculates its z coordinate based on the values of  each point and the scalar ccoef. That is, the expressions below take  x, y, and coef,  and returns a new point named newPoint  with the new z coordinate as indicated below.

More specifically, the outer loop expression for i in range(0, n + 1, 1)  generates a set of values for i, where  i = 0, i = 1, ... i =  n. The expression can be interpreted as start a loop with i set to the value of 0, (0, n + 1, 1), stop the loop when i reaches the value of n + 1, (0, n + 1, 1), and for each iteration through the loop increment the value of i by 1, (0, n + 1, 1).

The outer loop stops when i reaches value of n + 1, For each such outer loop value of  i, the inner loop expression for ii in range(0, n + 1, 1) generates a set of numbers ii = 0, ii = 1, ... ii =  n. The inner loop stops when ii is the value of n + 1.  For example, if n = 4,  we get the following sequence of values for i and ii:

 i = 0, ii  = 0
 i = 0, ii  = 1
 i = 0, ii  = 2
 i = 0, ii  = 3
 i = 0, ii  = 4

 i = 1, ii  = 0
 i = 1, ii  = 1
 i = 1, ii  = 2
 i = 1, ii  = 3
 i = 1, ii  = 4

 i = 2, ii  = 0
 i = 2, ii  = 1
 i = 2, ii  = 2
 i = 2, ii  = 3
 i = 2, ii  = 4

 i = 3, ii  = 0
 i = 3, ii  = 1
 i = 3, ii  = 2
 i = 3, ii  = 4
 i = 3, ii  = 5

If  pt1 is located at -1, -1, 0, coef = 0.5, n = 4,  deltaX = 0.5 and delta Y =0.5,  then we would get the x, y, z values for  20  points appearing in the plan view as follows:

OUTER LOOP 0  (first column of points in grid) index i = 0 , index ii = 0  ->  x = -1.0, y = -1.0, z = 0.0 index i = 0 , index ii = 1  ->  x = -1.0, y = -0.5, z = 0.375 index i = 0 , index ii = 2  ->  x = -1.0, y = 0.0, z = 0.5 index i = 0 , index ii = 3  ->  x = -1.0, y = 0.5, z = 0.375 index i = 0 , index ii = 4  ->  x = -1.0, y = 1.0, z = 0.0
OUTER LOOP 1  (second column of points in grid) index i = 1 , index ii = 0  ->  x = -0.5, y = -1.0, z = -0.375 index i = 1 , index ii = 1  ->  x = -0.5, y = -0.5, z = 0.0 index i = 1 , index ii = 2  ->  x = -0.5, y = 0.0, z = 0.125 index i = 1 , index ii = 3  ->  x = -0.5, y = 0.5, z = 0.0 index i = 1 , index ii = 4  ->  x = -0.5, y = 1.0, z = -0.375
OUTER LOOP 2  (third column of points in grid) index i = 2 , index ii = 0  ->  x = 0.0, y = -1.0, z = -0.5 index i = 2 , index ii = 1  ->  x = 0.0, y = -0.5, z = -0.125 index i = 2 , index ii = 2  ->  x = 0.0, y = 0.0, z = 0.0 index i = 2 , index ii = 3  ->  x = 0.0, y = 0.5, z = -0.125 index i = 2 , index ii = 4  ->  x = 0.0, y = 1.0, z = -0.5
OUTER LOOP 3  (fourth column of points in grid) index i = 3 , index ii = 0  ->  x = 0.5, y = -1.0, z = -0.375 index i = 3 , index ii = 1  ->  x = 0.5, y = -0.5, z = 0.0 index i = 3 , index ii = 2  ->  x = 0.5, y = 0.0, z = 0.125 index i = 3 , index ii = 3  ->  x = 0.5, y = 0.5, z = 0.0 index i = 3 , index ii = 4  ->  x = 0.5, y = 1.0, z = -0.375
OUTER LOOP 4  (fifth column of points g grid) index i = 4 , index ii = 0  ->  x = 1.0, y = -1.0, z = 0.0 index i = 4 , index ii = 1  ->  x = 1.0, y = -0.5, z = 0.375 index i = 4 , index ii = 2  ->  x = 1.0, y = 0.0, z = 0.5 index i = 4 , index ii = 3  ->  x = 1.0, y = 0.5, z = 0.375 index i = 4 , index ii = 4  ->  x = 1.0, y = 1.0, z = 0.0

And, aswill be described in PART 2,  if we were able to build the resulting hyperbolic parabolic surface for the given set of x, y, z values it would appear as illustrated below.

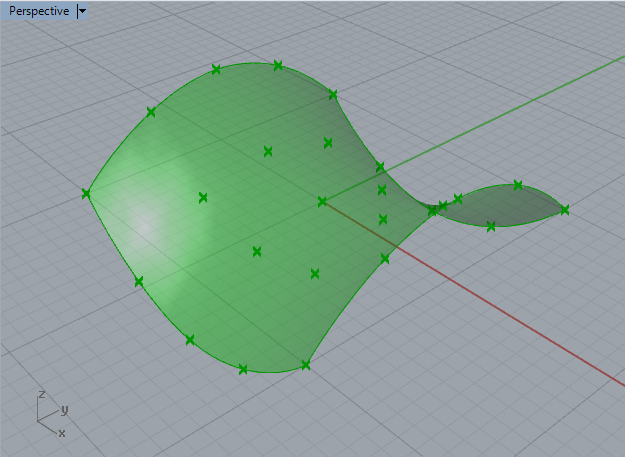
 Hyperbolic Parabolic Surface Based on 20 Points.

PART 2: Generating the Hyperbolic Paraboloid Surface From The 3D Points

To complete the implementation the hyperbolic parabolic surface, begin by placing corner points on the x-y ground plane  in Rhino at the location -1, -1, 0 and the location 1, 1, 0.

Next, as depicted in the figure below, within Grasshopper we initiate a setup by creating two corresponding "pt" components and two "number sliders". 

The slider named "coef" ranges in floating point coeficient values from -2.0, to 2.0 fto control the vertical scale of the hyperbolic parabolic surface, and the second slider named "n" ranges in number of surface division integer values from  2. to 40.

create a Python component with two "point3d" inputs, a  "float" input and an 'int" input similar to previous workshop notes, and then connect the corresponding parameters from the left side of the canvas window.

.

Add a output vaiable "b"  parameter to the Python component by zooming up close and selecting the "+" symbol similar to previous workshops.



Enter the Python component. Begin editing by importing the rhinoscirptsyntax library on line 4 similar to prior workshops. We also determine the incremental distance between grid points in the x and y axis by adding variables deltaX and deltaY, where  deltaX is the overall distance in the x drection divided by input variable n and

deltaY is the overall distance in the y drection divided by input variable n.

Continuing within the script editor,  add the double nested loop described in Part I above as depicted  lines 8 through 16 in the figure below.

Continuing within the script editor, we set the output variable "a" to the pointList as depicted  in line 18 in the figure below.

Finally,  add the rhinoscriptsyntax function AddSrfPtGrid as illustrated in lines 20 and 21 below. In line 20, we create a list named "count" which containts two elements, the count of points in the x direction and the count of points in the y direction. In turn, the AddSrfPtGrid function has two inputs, 1. the count of points in  X and Y direction, and  2. the ptList itself. The surface in turn is assigned to the output vaiable b.

The Grasshopper file and Phython scipt can be downloaded from the link here: hyperbolicParabolic.gh

PART 3: Surface Examples Created by Varying the Input Parameters

1. With the script setup in step 2, placing the corner pts at -10, -10, 0 and 10, 10, 0, adjusting the coeficient to 0.1,  and baking the output , yields a similar result at a greater plan dimrension.

2. Varying the coeficient parameter setup gives some of the following shapes (the view has been rotated to help see the resulting geometry).

coef = 0.1	coef = 0.25	coef = 0.5	cScalar =1

#Hyperbolic Parabolic Mesh z = coef * (pow(x, 2) - pow(y, 2))
#Eliptical Parabolic Mesh z = coef * (pow(x, 2) + pow(y, 2))
#Simple Saddle z = coef * (x * y)
#Sine Surface #Note: add the math library at the top of the script allows access the trignometry functions import math frequency = 2 z = coef * abs(math.sin(math.radians(x * frequency)))
#Sine Surface in X and Y frequency = 2    z = coef * abs(math.sin(math.radians(x * frequency)) + math.sin(math.radians(y * frequency)))
#Concentric Sine Wave dist = math.sqrt(pow(x,2) + pow(y,2)) frequency = 3 z = coef * abs(math.sin(math.radians(frequency * dist)))

In the last three examples the size of the plan is relative to the frequency of applying the sin or cos function relative to the given scale. For example, we can rewrite the scipt and adjust the parameters as follows if the corner points are still located at -1, -1, 0 and 1, 1, 0. The values of coef = 0.025 and of n = 20.



Within the script itself add the math library in line 4 and then setup for the trignometic functions in lines 15 through 17

The baked result in Rhino concentrates the sine waves in the area delimited by the corner points -1, -1, 0 and 1, 1, 0 and when rebuilt with a 50 x 50 point count appears as follows: The Grasshopper file and Python link can be downloaded from here. ConcentricSinWavSurf.gh.

Summary

Within this workshop we have developed a few basic scripts for representing three-dimensional surfaces . The principal building block of these surface elements has been  various kinds of polynomial based surfaces. The examples also demonstrate the power of encapsulating the basic parameters of a particular architectural composition within a few variables. In the case of polynomial related surfaces, we were able to succinctly describe the range of the surface between two coner points, the scale of its curvature (i.e., the variable coef) and the resolution of its curvature (i.e., the variable n).