These notes introduce the use of function definitions inside of Python components within Grasshopper.
1. Hello World and Simple Python Scripts
In some circumstances it may be effective to use a Python script component in conjunction with other Grasshopper components. We begin with a few simple Python scripts. These first scripts are for introductory purposes and don't necessarily offer an advantage in terms of efficiency or clarity over other Grasshopper components. We will then move onto Python scripts which do offer advantages over other Grasshopper options in terms of conciseness and clarity of organization. Within these examples we take advantage of libraries and related function calls to perform some tasks, such as:
a
= rs.AddLine(point1, point2)
The above expression assigns to the variable "a" a line. The line
generated by a function called "AddLine" that is located in
"rhinoscriptsyntax" library
abbreviated
here as "rs". "AddLine" creates a line from two
existing end points, which in the above example are named "point1" and
"point2". More complete documentation on Python, examples, and
associated
libraries are located at the web site
http://wiki.mcneel.com/developer/python.
More specifically Rhino graphic libraries used in the examples are:
Rhino Common Libary - library functions for Rhino Python, most of which are also available to the Python scripting component within Grasshopper. This library is referred to as "Rhino" in the examples we will cover in the workshop notes.
Rhino Script Syntax Library - library functions
for Rhino Python, most of which are also availble to the Python
scripting component within Grasshopper. This library is referred to
as "rhinoscriptsyntax" in the examples we will cover in the workshop notes.
Note for now that the Rhino Common Library has geometry elements with a data structure that is the same as the entities created directly in with direct Rhino comands. However the Rhino Script Syntax Libary has geometry has elements that contain an alternative data structure that is optimized for scripting in inside Python. These "rhinoscriptsyntax" elements are converted to direct Rhino entities if output from Python to Rhino. This distinction between the two libraries will be clarified in workshop notes 11.
For published tutorials and manuals see:
The RhinoPython 101 manual. - step by step tutorials are at the end of pdf file primer
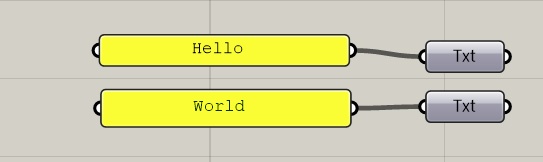
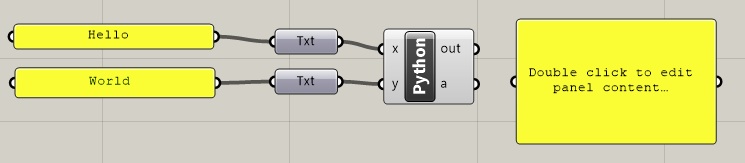
To get started, launch Rhino and Grasshopper, and then within Grasshopper load the file helloWorld.gh. The file shows two Python scripts, one that takes as input a text strings such as "Hello World!" and echoes it back, and the other that takes as input two numbers and outputs their sum.
In the case of "Hello World!", the Python examples follows a tradition of introducing programming languages that usually start with a function that prints or echos the words "Hello World!" back to the user.
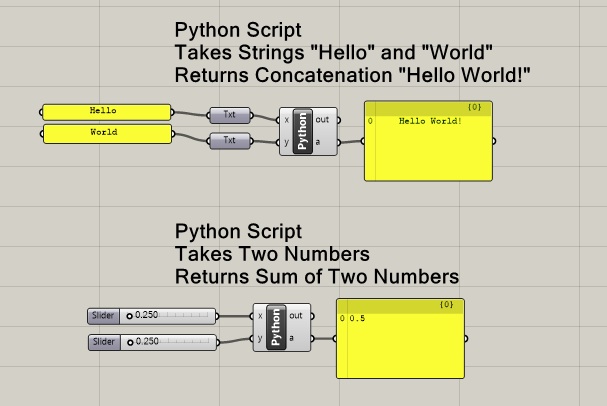
Note in the above illustrated canvas window that the input text strings "Hello" and "World" appear in separate yellow text boxes. In turn the yellow text boxes are connected to the input port of two "Txt" (string) Grasshopper components. The two "Txt" components are in turn connected to the Python script input parameters "x" and "y".
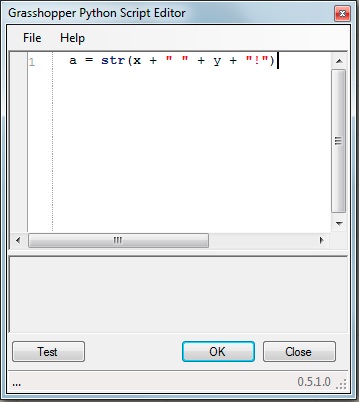
To see the Python Script in detail, double click on "Python" icon in the Grasshopper window to launch the script editor. The first line of Python script, as shown below, adds the two strings together and places an exclamation mark a the end. The same expression also assigns it to the output variable "a".
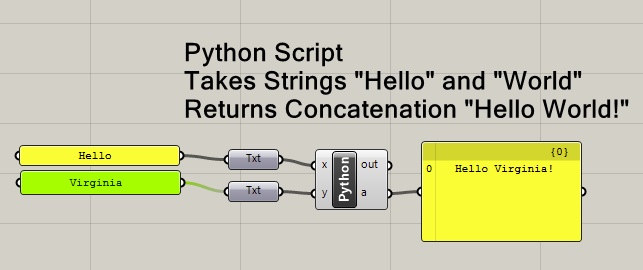
The Python component in turn returns the parameter "a" through an output port into the input port of the yellow text box which is placed to the right of it in the canvas window as depicted below. The yellow text box echoes back the text string "Hello World!". However, if you modify either of the input text strings, then the output text string is modified accordingly, such as replacing the text string "World" with the text string "Virginia" in the example below.
Note above that the two input arguments "x" and "y" are passed into the Python script component as strings ("Str"). The string designation means that both "x" and "y" are can be assigned a text expression consisting of alphanumeric characters.
Note
too that any change to the value of an input variable (such as "x" or
"y") inside the Python Script component is limited in scope
to be internal to the script function. That is, the modification
to the value of the variable internal to script function would
not change its value outside the script. Thus if inside the
Python component we add the expression y = "virginia film festival".
the value of y outside of the script would be unchanged from
"Virginia".
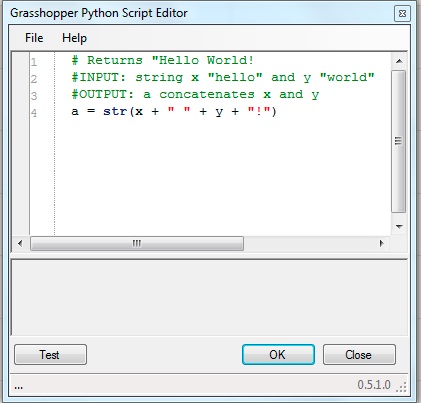
Lets go into more detail regarding the Python component shown above. The expression in line 1 is:
a =
str(x +
" " + y + "!")
The statement assigns a string value to variable "a" by joining
together four values:
1. the value of the string x,
2. a blank space " ",
3. the
string y, and
4. the exclamation point "!".
Note that the use of the
"+" symbol is used to add together (concatenate) the larger string from
the four values "Hello", " ", World, "!", similar to how one might add
several numbers together. Once again, the variable "a" is also the output variable of the script. Thus, it in
turn is directed to the input port of the yellow panel that displays
the result "Hello World!".
Now we will reconstruct the script from scratch. Go to File/New Script.
Go to the "Params" tab and in the "Input" area, select the
yellow
panel.
Drag two yellow panels with the left-mouse button into the Grasshopper
view window.
Double click on each panel, and edit the text string to
become
"Hello" on on panel and to become "World" on the
other
panel.
The result is that the panels should transform as follows.
Continuing with the "Params" tab, go to the
"Primitive"
area and select the string component symbolized by the letter "A".
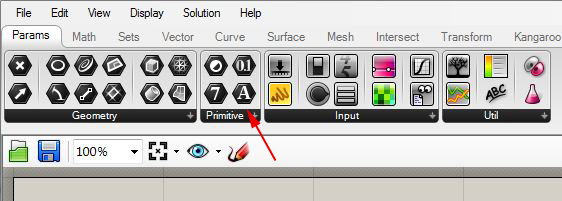
Drag two string components with the left-mouse button into the
Grasshopper view window, and connect their input ports to the output
ports of the two yellow panels.
In the more recent release of Grasshopper the "A" symbol is referred to
as with the label "txt" in the in the Grasshopper cavas window below.
Now go the the "Math" tab and in the "Input" area, select the blue and
yellow Python component.
Drag
on
Python component with
the left-mouse
button into the Grasshopper view window and connect its input
ports to the output ports of the two string components.
Resize
the yellow panels by moving the mouse over any of its edges, depressing
the left-mouse button, and dragging the edge to the desired size.
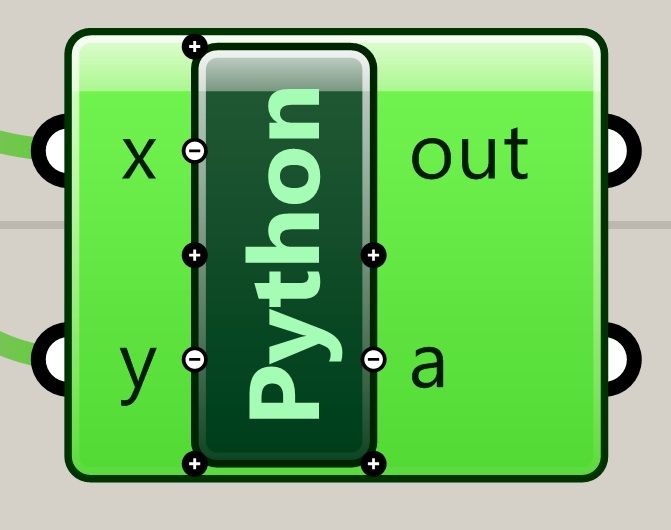
Zoom into the Python component , right-click on the letter
"x",
go the the "Type hint" item, and change the type to "String". Do the
same for the letter "y" variable.
Now, double-click on the Python component symbol in order to open it script editor. Note that it is essentially an emptry text file.
Type
in the
single expression needed to complete the script.
a = str(x + " " + y + "!")

Select the "OK" button on the lower right hand corner of the script
editor to conclude editing the script. Go back to the "Params" tab and
to the "Input" area, select the yellow panel , add it to the
right of
the Python script within the Grasshopper view window.
Connect the output port "a" of the Python script to the yellow panel to
see the output.
Note that it is generally quite useful t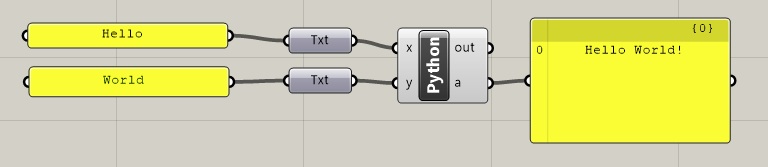 o document the purpose and the input
and output variables of the Python script with comment lines. Comment
lines are not executed and are preceded by a number symbol # (e.g., #This
is a comment
line). For
example, double-click on the Python component,
and add the comment lines:
o document the purpose and the input
and output variables of the Python script with comment lines. Comment
lines are not executed and are preceded by a number symbol # (e.g., #This
is a comment
line). For
example, double-click on the Python component,
and add the comment lines:
#Returns
"Hello World!
#INPUT:
string x "hello" and y "world"
#OUTPUT: a
concatenates x and y
The Python script to construct two numbers is constructed in a similar
way. Go to the "Params" tab and from the "Input" and a number slider.
Drag two number sliders into the Grasshopper view window. Now, similar
to the "Hello World" example, go to the Math "Tab" and from the
"Script" area drag Python component with the left-mouse
button
into the Grasshopper view window and connect its input ports to the
output ports of the two number slider components.
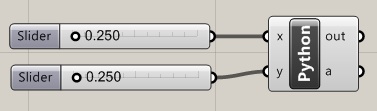
Zoom into the Python component , right-click on the letter
"x",
go the the "Type hint" item, and change the type to "Double". Do the
same for the letter "y" variable. Double click on the Python symbol in
order to open the editor. Note once again that the editor is
essentially an empty file.

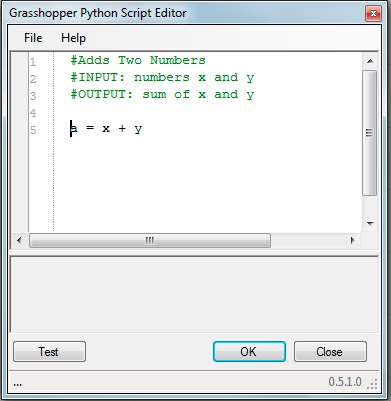
The following comment lines and expressions are now added to complete
the script and return the result in the variable a.
#Adds
Two Numbers
#INPUT:
numbers x and y
#OUTPUT:
sum of x and y
a = x + y
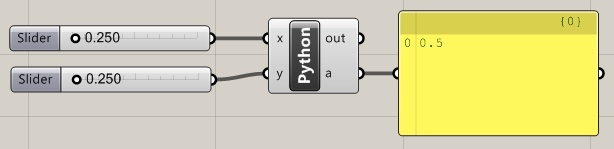
Finally,
select the "OK" button on the lower right hand corner of the script
editor to conclude editing the script. Go back to the "Params" tab and
to the
"Input" area, select the yellow panel , add it to the right of the
Python
script within the Grasshopper view window. Connect the output
port "a" of the
script to the input port of yellow panel to obtain the final result of the script.
2.
Scripts to Draw a Few Graphic Primitives
Here we perform a simple task of creating a line by using a Python script. This is also illustrated in the grasshopper file makeSimpleLine.gh.
Initiate the script within Rhino by creating two points in the x, y ground plane.
Within Grasshopper, go to the "Params" tab and within the "Geometry" area, select and drag two point icons into the work area.
Right-click on each of the two points and use the "set on point" option to connect them to the points created on the x, y plane.
Next, similarly to "Hello World" example above, go the "Math" tab and within the "Script" area drag a "Python" component into the Grasshopper View window.

Double-click on "Python" of the Python scripting component, go to the script editor, and add the following expressions:
Add the following lines to load relevant software libraries
import
rhinoscriptsyntax as rs
import
Rhino as rc
import
math
Add
the following
comment lines at the beginning of the script:
#Draws
a
linefrom two points
#sINPUTS: Two points
#OUTPUT: A line determined by the two points
Add the following statements after the comment lines:
a
= rs.AddLine(point1, point2)
Within the script editor we see the following result:
This completes the script and resulting line should now appear inside Rhino.
Move either of the two points and the line is modified accordingly.
The same script can be modified to draw a rectangle, makeSimpleRectangle.gh, from the initial end points.
First, note that we can extract the coordinates x1, y1, z1 from point1 and the coordinate x2, y2, and z2 from point2. We can combine the two sets of coordinate to get the four points cornerPt1, cornerPt2, cornerPt3 and cornerPt4, that detemine the rectangle. Assuming that both point1 and point2 are in the x-y plane, also note that z1 = z2 = 0. That is, we have the following way to establish the values of the four corner points.
cornerPt1
- based
upon x1, y1, z1
cornerPt2 - based upon x2, y1, z1
cornerPt3 - based upon x2, y2, z1
cornerPt4 - based upon x1, y2, z1.
With this in mind, we can edit the Python script as indicated below to get a rectangle. Note that comment lines added to the script describe what is achieved by each step.
#'Draws
a
rectangle from two points
#'INPUTS: Two points
#OUTPUT: A rectangle (polyline) determined by the two
points
#Create
the
corner points from the
x, y, and z coordinates of
point1 and point2
cpt1 = rc.Geometry.Point3d(point1.X, point1.Y, point1.Z)
cpt2 = rc.Geometry.Point3d(point2.X, point1.Y, point1.Z)
cpt3 = rc.Geometry.Point3d(point2.X, point2.Y, point1.Z)
cpt4 = rc.Geometry.Point3d(point1.X, point2.Y, point1.Z)
#Add
the
first corner point from the
x, y, and z coordinates of
point1 to complete the polyline
cpt5 = rc.Geometry.Point3d(point1.X, point1.Y, point1.Z)
#Create
the polyline from the
list of points
line1 = rs.AddPolyline([cpt1, cpt2, cpt3, cpt4, cpt5])
#Return the polyline
from the Python script
a = line1
The
script editor
is now modified as follows.
The script as now completed draws a rectangle. Note that moving the lower left corner point from within Rhino dynamically redraws the rectangle.
Looking at this script in greater detail, observe that we have embedded a point list [cpt1, cpt2, cpt3, cpt4, cpt5] withing the statement
line1 = rs.AddPolyline([cpt1, cpt2, cpt3, cpt4, cpt5])
We add the lower-left point to both the beginning and the end of the list to ensure that we get a closed polyline..Note too that we introduced a polyline object variable with the statement line1 = rs.AddPolyline
The polyline object line1 is thus initialized with the listing of points.
3. Script That Uses Iteration to Draw a Polygon or Circle
To draw a polygone this script begins with establishing the basic input parameters of center point, number of sides, and radius. Open Grasshopper and enter two numerical sliders to detemine the number of sides of the for the polygon from 3 to 360, and the number value of the radius from a minimum of 0.2 to a maximum of 300, by working with the numerical sliders first introduced in part 1. above.
For the number of sides, create a slider with the values specified as follows:
Similarly, ror the number of radius, create a slider with the values specified as follows:
Next create a point within Rhino to determine the origin of the circle and connect it to a point input parameter within Grasshopper similar to the technique used in part 2 above.
Now add a Python script component with inputs for Number of Sides, Radius and the Center Point of the circle.
Right-click on each of the input parameters and in turn establish an "int" hint for "numberSides", a "float" hint for "radius" and a "Point3d" hint for "centerPt". Next, connect the input parameters to the Python component.
Note that the "while" loop repeats lines 20 through 26 until the condition of curAngle <= 360 is exceeded. The value of "curAngle" is incremented each time through the loop by value of "deltaAngle". The variable "curAngle" is thus used to ensure that the while loop comes to conclusion. Otherwise, the loop would continue indefinitely and the program would effectively freeze. This is sometimes referred to as an infinite loop.
Adding a new input variable "radiusIncrement" can be used to convert the above procedure to generate an Archimedes curve (see number 7 below). In addition, adding a second new input variable "radiusAccelearation" can be used to convert the above procedure to generate an outward accelerating curve similar to a logarithmic spiral.
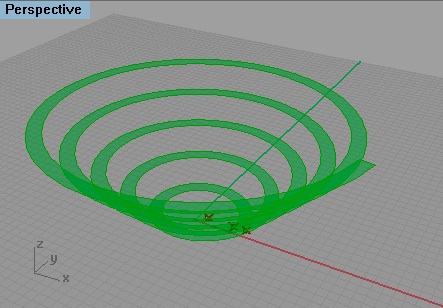
4. Script That Uses Iteration to Generate A Helix
To draw a series of inwardly rotating polylines form the outer rectangle, we needed to repeat a similar operation a specified number of times. Similar to the rotating figure above, a helix, such as determined by, adjustableHelixPython.gh, can also be described by a loop. The vertices that are used to define the spiral are also created in a repeated operation for a specified number of times.
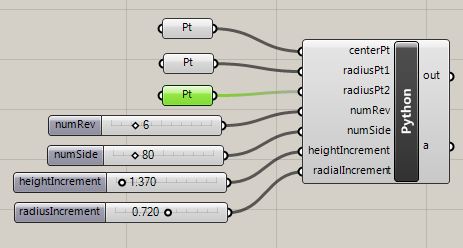
Using tools described previously, initiate the helix by placing two point parameters with a Grasshopper window, and by also adding four numerical slider parameters. One point will be used to identify the center of the spiral. The second point will be used to define the radius. The following sliders should have the following value types and ranges:
| Name of Slider | Description | Type | Min Value | Max Value |
| numRev | number of revolutions in the spiral | Integer (N) | 1 | 25 |
| numSide | number of sides in each revolution of the sprial | Integer (N) | 3 | 360 |
| heightIncrement | height increment in each revolution of the spiral | Floating Point (R) | 0 | 25 |
| radiaIncrement | radius increment in each revolution of the sprial | Floating Poing(R) | -25 | 25 |
Next, connect the points in Rhino to the point
input
parameters, as done
in previous examples. The two points will serve as the center point and
radial point of the sprial.
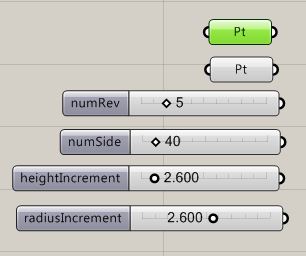
Now, add a Python script component to the Grasshopper View window and add the following input variables and types (use the Type hint feature as done in earlier examples):
| Name of Variable | Description | Type hint |
| centerPt | center point of helix | Point3d |
| radiusPt | radial point of helix | Point3d |
| numRev | number of revolutions in the spiral | int |
| numSide | number of sides in each revolution of the sprial | int |
| heightIncrement | height increment in each revolution of the spiral | float |
| radiaIncrement | radius increment in each revolution of the sprial | float |
Note that the sliders for numRev and numSide ares specified at int (integers), but that the input variables numRev and numSide are specified as float (i.e. floating point numbers). Thus the values are converted from integers to floating point numbers when connected to the Python script. The integer designation for the sliders ensures that only whole numbers are selected. This conversion to floating point numbers ensures that floating point accuracy is maintained in the Python script where needed in some operations.
Finally, double-click on the Python script and add the following expression into the script editor.
import
rhinoscriptsyntax as rs
import Rhino as rc
import math
#draws
a helix
#INPUTS:
#centerPt
and radiusPt of helix
#numRev
= number of revolutions
in helix
#numSide
= number of sides per
revolution
#heightIncrement
= height
increment per revolution
#radialIncrement
= radius
increment per revolution
#OUTPUT:
#a
= pline = polyline
approximation of helix curve
#Declare
variables for spiral
point list, vector from center pt to radius pt, and radius
ptList = []
radialVector = rs.VectorCreate(radiusPt, centerPt)
radius = rs.VectorLength(radialVector)
#Declare
variable to hold
incremental values of rotation angle, height and radius for each point
in the spiral
angleIncrement = 360.0/numSide
ptHeightIncrement = heightIncrement/numSide
ptRadialIncrement = radialIncrement/numSide
#Declare
variable to hold the
initial values for the angle, height and radius
curAngle = 0
curHeight = 0
curRadius = radius
#Loop
to generate points in the
spiral
i = 1 #initiate counter for loop
while ( i < numRev * numSide) :
....x = centerPt.X +
math.cos(math.radians(curAngle)) *
curRadius
....y = centerPt.Y +
math.sin(math.radians(curAngle)) *
curRadius
....z = centerPt.Z + curHeight
....curPt = rs.AddPoint(x, y, z)
....#Add each
successive point to the point list
.... ptList.append(curPt)
....
....#Advance the
values of the current angle, current height and current radius for the
next point in the spiral
....curAngle = curAngle + angleIncrement
....curHeight = curHeight + ptHeightIncrement
....curRadius = curRadius + ptRadialIncrement
....i = i + 1 #increment loop counter
#Determine
a polyline from the
point list
pline = rs.AddPolyline(ptList, replace_id=None)
#Return
the polyline to Rhino
a = pline
Select the "OK" button in the editor and the Grasshopper file will produce the helix as depicted in the following image.
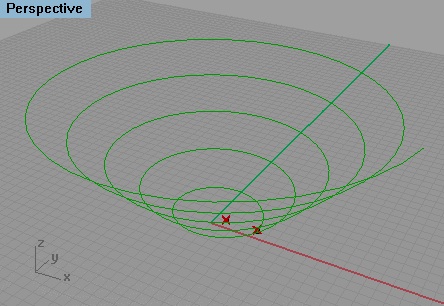
5.
Script That Uses Iteration to Generate A Ramp
The helix script can be enhanced to become todraw two spirals that form a ramp, as illustrated by the Grasshopper file adjustableRampPython.gh.The essential strategy for looping through vertices is the same. Begin by adding a radial point within Rhino to determine the location of the second helix.
Next, within Grasshopper add a new point input parameter radialPt2 and
connect it to the recently added radial point, and a corresponding
Point3D variable "radiusPt2" to the Python script.
Within the Python script, we now double up on the points so as to produce two spirals rather than one spiral. Furthermore, rather than use the points to form a polyline as in the previous example of the helix, we use them to form two bspline curves. Next, the bspline curves are used to generate a ruled surface. Whereas polylines can not be used to generate a ruled surface, the bspline curves can be used to generate one.
The
Python scrip
is
modified as follows. See the comment lines below for details:
import
rhinoscriptsyntax as rs
import Rhino as rc
import math
#draws
a helix
#INPUTS:
#centerPt
and radiusPt of helix
#numRev
= number of revolutions
in helix
#numSide
= number of sides per
revolution
#heightIncrement
= height
increment per revolution
#radialIncrement
= radius
increment per revolution
#OUTPUT:
#a
= pline = polyline
approximation of helix curve
#Declare
variables for spiral
point list, vector from center pt to radius pt, and radius
ptList
= []
ptList2 = []
radialVector = rs.VectorCreate(radiusPt1, centerPt)
radius1 = rs.VectorLength(radialVector)
radialVector2 = rs.VectorCreate(radiusPt2, centerPt)
radius2 = rs.VectorLength(radialVector2)
#Declare
variable to hold
incremental values of rotation angle, height and radius for each point
in the spiral
angleIncrement = 360.0/numSide
ptHeightIncrement = heightIncrement/numSide
ptRadialIncrement = radialIncrement/numSide
#Declare
variable to hold the
initial values for the angle, height and radius
curAngle = 0
curHeight = 0
curRadius = radius1
curRadius2 = radius2
#Loop
to generate points in the
spirals
i = 1 #initiate
counter for loop
while ( i < numRev * numSide) :
....x = centerPt.X +
math.cos(math.radians(curAngle)) *
curRadius
....y = centerPt.Y +
math.sin(math.radians(curAngle)) *
curRadius
....z = centerPt.Z + curHeight
....curPt = rs.AddPoint(x, y, z)
....x2 = centerPt.X +
math.cos(math.radians(curAngle)) *
curRadius2
....y2 = centerPt.Y +
math.sin(math.radians(curAngle)) *
curRadius2
....z2 = centerPt.Z + curHeight
....curPt2 = rs.AddPoint(x2, y2, z2)
....
....#Add each
successive point to the point list
....ptList.append(curPt)
....ptList2.append(curPt2)
....
....#Advance the values of the current
angle, current
height and current radius for the next point in the spiral
....curAngle = curAngle + angleIncrement
....curHeight = curHeight + ptHeightIncrement
....curRadius = curRadius + ptRadialIncrement
....curRadius2 = curRadius2 +
ptRadialIncrement
....i = i + 1 #increment loop counter
#Determine
a polyline from the
point list
pline = rs.AddPolyline(ptList, replace_id=None)
pline2 = rs.AddPolyline(ptList2, replace_id=None)
#Build
lofted surface between
two curves
rampSurf = rs.AddLoftSrf([pline, pline2])
a = rampSurf
fvv#Build
lofted surface between two curves
rampSurf = rs.AddLoftSrf([pline, pline2])
In particular we used a function library "rs.AddLoftSrf". A number of functions have been created for Grasshopper to generate geometry and handle other requirements. The current listing of functions and related examples can be found in the web site: http://wiki.mcneel.com/developer/python
A set of notes in PDF file format has also been developed here for an overview to be presented directly in class.