|
Date:
February 5, 2009 |
Arch
544: Parametric Rapid Prototyping |
The procedures referred to in these problems are simple in the sense of not relying upon any advanced programming structures. The last extra credit problem, taken from Serlio, is not simple in geometry, but is simple in the kind of steps needed to execute its construction.
Problem 1
Write the Point graphics function mid-point.gct below that finds the location of a point mid-way between two points and prints the result. This procedure is complete. You need to only replicate it and test it in GC. The technique of finding a mid-point will be useful in other procedures that follow this one.Note the liberal use of comment lines that help you the reader to understand the steps in the procedure. You need not submit this procedure as a part of the homework assignment, only test it. The GC file mid_point.gct can be downloaded to double-check your work.
| function ( ){ //Find the mid-point of two points Point point1 = new Point(); Point point2 = new Point(); Point midPoint = new Point(this); double xval, yval, zval; //Assign initial values to points. These values are arbitrary. xval = 0.0; yval = 0.0; zval = 0.0; point1.ByCartesianCoordinates(baseCS, xval, yval, zval); xval = 55.0; yval = 50.0; zval = 0.0; point2.ByCartesianCoordinates(baseCS, xval, yval, zval); //Compute average and detemine mid-point xval = (point1.X + point2.X)/2.0; yval = (point1.Y + point2.Y)/2.0; zval = (point1.Z + point2.Z)/2.0; midPoint.ByCartesianCoordinates(baseCS, xval, yval, zval); //Print out the result to the Console window Print("The mid-point is " + midPoint.X + " " + midPoint.Y + " " + midPoint.Z + "\n"); } |
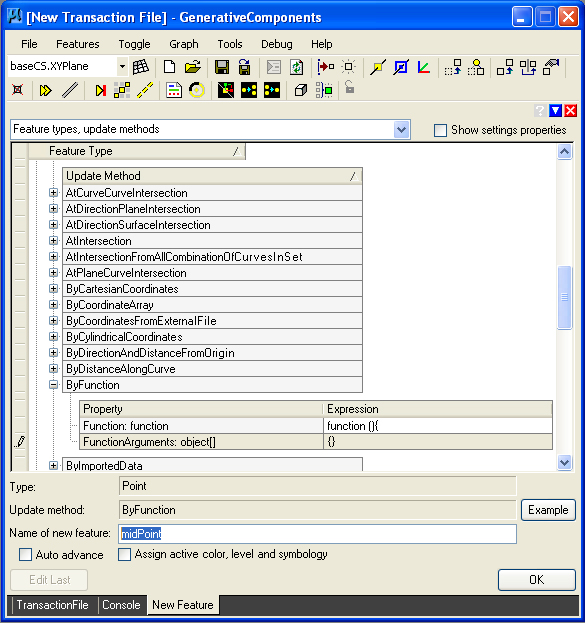
To implement this function call within GC, we begin with creating a Point feature via a function description. Note that we can enter "midPoint" in the text box for "Name of the new feature" .

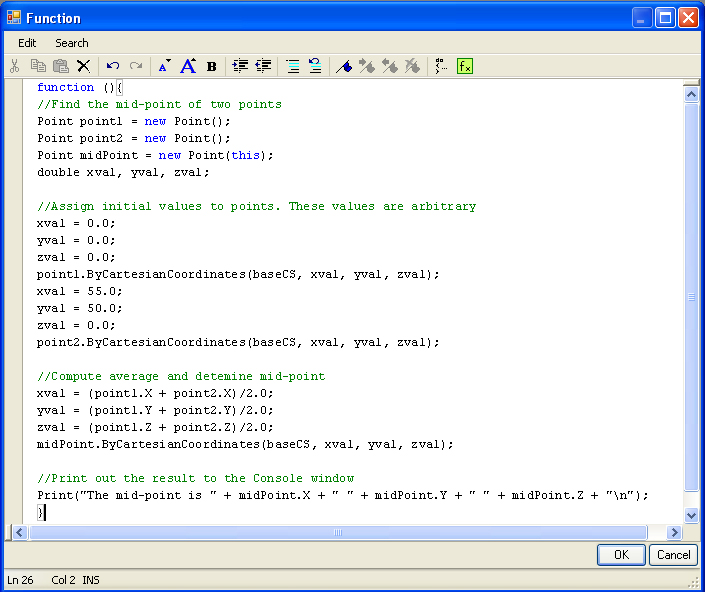
The function contains no arguements, and is edited via the function text box (see Chapter 2 for details on this step).
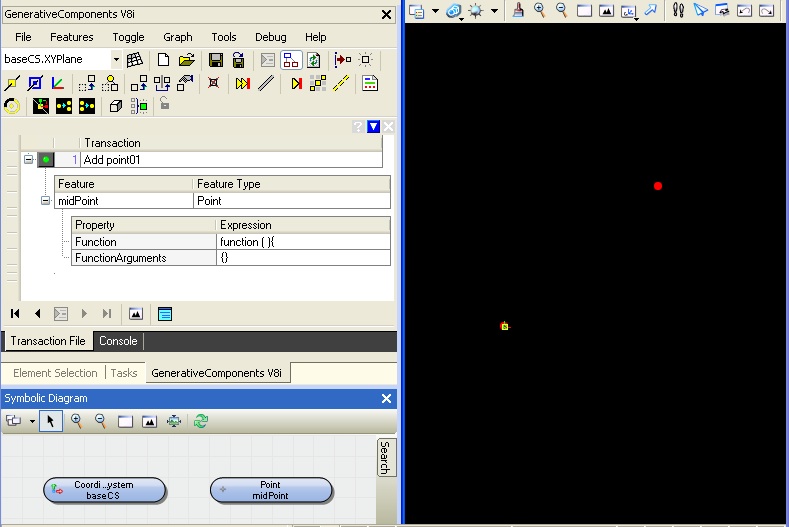
Within the Transaction File Tab, record the function so as to obtain the following result (see chapter 2 for more details on this step).
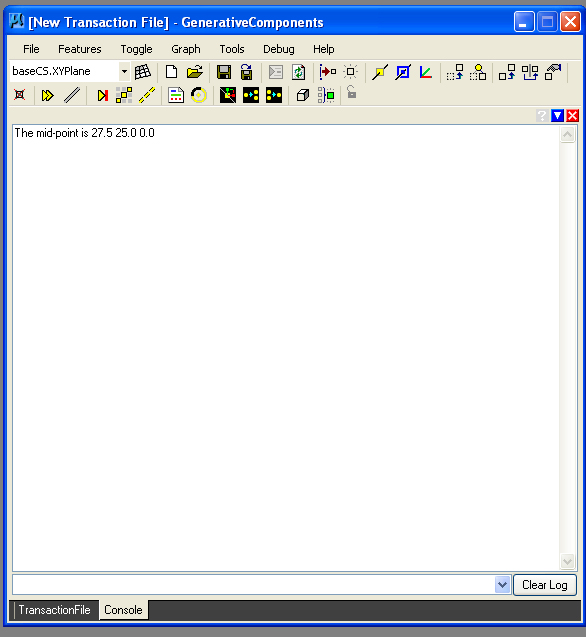
Note that printing to the console tab, yields the following output, a way of double-checking the calculation of the function.
Problem 2
Re-develop the GC procedure below as a PolyLine function that draws a rectangle from a set of four points. Note that it contains a variable length that is not actually used (a flaw). How can you modify this program such that length is used throughout it? That is, edit the program such that it performs draw-rec from four points using the length variable. Test the program in GC and save it to your homework submit directory under the name draw-rec.gct.

| function(){ // draw a square of given length //allocate memory for points, lines and necessary values Point startPoint = new Point(); Point point1 = new Point(); Point point2 = new Point(); Point point3 = new Point(); Point point4 = new Point(); PolyLine a_square = new PolyLine(this);//keyword 'this' means primary entity of the function double xval, yval, zval, length; // locate the startPoint at the origin xval = 0.0; yval = 0.0; zval = 0.0; startPoint.ByCartesianCoordinates(baseCS, xval, yval, zval); // determine the length of the square length = 4.0; // create lower left corner point of the square // this is actually the same as startPoint - could rewrite the procedure without it xval = startPoint.X; yval = startPoint.Y; zval = startPoint.Z; point1.ByCartesianCoordinates(baseCS, xval, yval, zval); // create lower right corner point of the square xval = startPoint.X + 4.0; yval = startPoint.Y; zval = startPoint.Z; point2.ByCartesianCoordinates(baseCS, xval, yval, zval); // create upper right corner point of the square xval = startPoint.X + 4.0; yval = startPoint.Y + 4.0; zval = startPoint.Z; point3.ByCartesianCoordinates(baseCS, xval, yval, zval); // create upper left corner point of the square xval = startPoint.X; yval = startPoint.Y + 4.0; zval = startPoint.Z; point4.ByCartesianCoordinates(baseCS, xval, yval, zval); // determine a new PolyLine based upon the four points // note: list of points is contained in curly brackets a_square.ByVertices({point1, point2, point3, point4, point1}); } |
Problem 3
Write a program draw-tri.gct that draws a triangle from any three points. Save it to your homework submit directory.
More specically, your task is to complete the program partially completed below and then to revise it. The revised program should make use of the three Points point1, point2 and point3 in the description of the triangle. Note too that the variable startPoint could be removed in your version of this program. That is, your goal is to modify the program such startPoint is eliminated.
 |
| function() { // simple procedure to draw a triangle //Set aside memory for points and values Point startPoint = new Point(); Point p1 = new Point(); Point p2 = new Point(); Point p3 = new Point(); double xval, yval, zval; PolyLine a_triangle = new PolyLine(this); // establish starting point at origin xval = 0.0; yval = 0.0; zval = 0.0; startPoint.ByCartesianCoordinates(baseCS, xval, yval, zval); // establish lower left hand corner of triangle xval = startPoint.X; yval = startPoint.Y; zval = startPoint.Z; p1.ByCartesianCoordinates(baseCS, xval, yval, zval); // establish lower right hand corner of triangle xval = startPoint.X + 4; yval = startPoint.Y ; zval = startPoint.Z; p2.ByCartesianCoordinates(baseCS, xval, yval, zval); // establish apex of triangle xval = startPoint.X + 2; yval = startPoint.Y + 2; zval = startPoint.Z; p3.ByCartesianCoordinates(baseCS, xval, yval, zval); //create the triangle -< what code is needed here to complete the program (see end of problem 3) } |
Problem 4
Write a procedure that given three points will draw two triangles: an outer triangle and then a triangle which is determined by the mid-points of the line segments of the outer triangle as in the illustration below. Do this combining the logic of the program mid-point.gct with the logic of the program draw-triangle.gct. Add the GC programming language expressions needed and then test the procedure. Save the program in your submit folder as draw-triangle2.gct.
 |
Problem 5: Extra Credit
Part I: Within his book on Geometry, Serlio describes several methods for drawing an oval (on reserve in the Fine Arts Library). Write a simple graphics procedure that recreates any of these methods.from Serlio excerpted in the table below (parenthesis added). Note that if you are viewing this page from a World Wide Web browser , you may excerpt a copy of the GC procedure in the third column . The oval shape has the superficial appearance of an elipse, however, it is not quite the same. Note that we might think of elipse as a "particular oval shape" with "a more precise mathematical description" (from Oxford dictionary of mathematics). You need not actually turn in this code as a part of the assignment. Rather, keep the more extended development of this code in mind as you write code for your own pattern.
Part II: Similar to the example of the oval, examine the pattern you developed for exercise two and write a procdure to generate some part of or all of the pattern. Save the work into the submit directory as mypat.bas.
| Serlio's Description | Labeled Diagram | Procedure |
| "Draw three circles in the way shown below (drawing to the right). By drawing the four straight lines, its centres will be I, K, L, M. Place one point of the compasses on K, extend the other point to I and then arc round to 2. In the same way, place one point of the compass on the point I, the other on 3 and arc round to 4. This will form the oval shape. This shape is very similar to the natural egg." |  |
GC |
| "The method for drawing the third oval shape, shown below (drawing to the right), is this: draw two perfect squares joined together; draw in the diagonal lines to make the two centres in the middle G, H - the two other centres will be E, F: place, then, one of the compass points on F, the other on 1 and arc round to 2; then do the same at the centre E and arc round from 3 to 4. Next place one compass point on the centre G, extend the other to 1 and circle around to 3. Do the same at the centre H, extend the compass point to 2 and draw around to 4. The shape as shown below will be formed." |  |
GC |
| "If you wish to form this fourth oval shape, draw two circles such that each touches the centre of the other. At the intersections of the curved lines make two centres N, O. At the centres of the circles make two other centres P, Q. Draw lines connecting the centres. Place one compass point on the centre O, the other point on 1 and draw the curved line to 2. Then put one of the compass points on the centre N, the other on 3 and arc around to 4. This oval shape will be formed. It is very pleasing to the eye and should be used for many things because it is so easy to draw and because of its elegance." |  |
GC |
What you need hand in:
1. Save and name your Macro procedures into your "submit" sub-directory
through the GC save transaction file procedures that we will cover in
class.
2. Send email to Earl Mark ejmark@Virginia.edu and to both David Malda dcm9b@virginia.edu and Michael Plehn mep4d@virginia.edu that describes the work you have done. Submit a few paragraphs documenting your research and any observations you may have made.
We will show you how to do all of this in section. Feel free to consult in person or by email should you be in need of assistance.
What is to come:
In the coming chapters we shall consider how geometry may be encoded using the GC scripting language to structure some of the relationships that recur between graphics elements with some compositions.. We see in example 5 above such a relationship in the method of drawing the inner from the outermost triangle.We will investigate some more consise methods for how you might handle a series of such triangles.